問題PDF
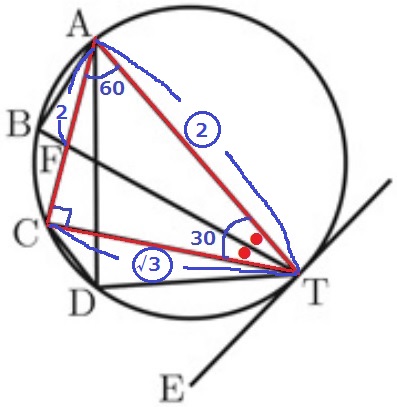
図のように点Tで直線TEに接する円がある。
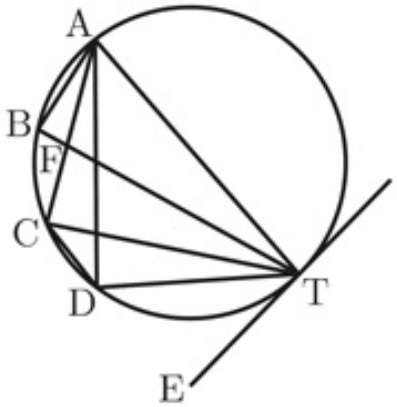
4点A、B、C、Dは円周上の点で、∠ATDは弦BT、CTにより3等分されている。
線分ACとBTの交点をFとし、AF=2、∠TAB=75°、∠TCD=45°として、
次の問いに答えなさい。
(1)
∠DTE、∠ATDの大きさを求めなさい。
(2)
AT:CTを求めなさい。
(3)
FCの長さを求めなさい。
(4)
円の半径rの長さを求めなさい。
@解説@
(1)
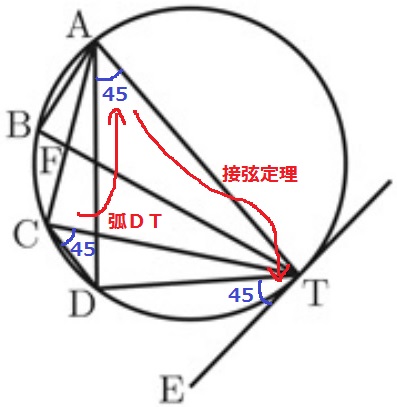
↑使うべき情報だけを記入しました。
弧DTに対する円周角で∠DAT=45°
接弦定理より、∠DTE=45°
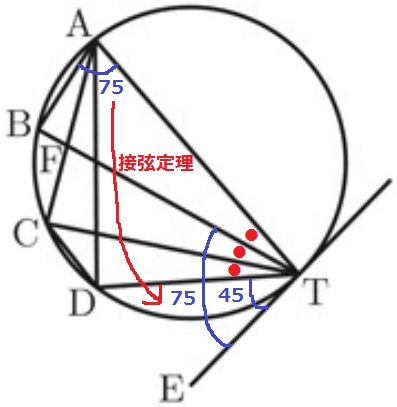
弦BTで接弦定理→∠BTE=75°
∠BTD(●●)=75-45=30°
∠ATD(●●●)=30×3/2=45°
(2)
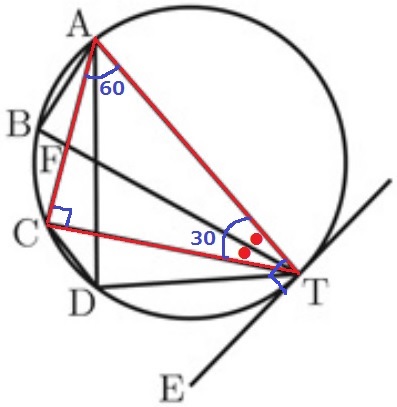
AT:CTを求めたいので、それらを1辺とする△ACTに着目する。
∠ATC(●●)=30°
前問で∠DTE=∠ATD=45°と求めたので、∠ATE=90°となり、
ATは接線TEに対して垂直→ATは円の直径
半円の弧に対する円周角で、∠ACT=90°
△ACTの内角は30°-60°-90°で、辺の比が1:2:√3の直角三角形。
AT:CT=2:√3
(3)
長さを求めるので、ここでAF=2を利用する。
角の二等分線の定理。
TA:TC=AF:FC=2:√3
FC=2×√3/2=√3
(4)
AC=2+√3
△ACTの辺の比でAC:AT=1:2から、
ACを2倍して直径AT、それを÷2して半径rがでる。
r=(2+√3)×2÷2=2+√3



コメント