問題PDF
座標平面上を3つの動点P、Q、Rが原点Oを同時に出発し、
以下のような経路で毎秒1の速さで動く。ただし、点と点の間は最短経路を進むものとする。
動点P:原点O→点(0、4)→点(2、4)→点(2、6)→点(0、6)
動点Q:原点O→点(-2、0)→点(-2、2)→点(0、2)→点(0、4)→点(2、4)
動点R:原点O→点(6、0)→点(2、0)
原点を出発してからt秒後の△PQRの面積をyとするとき、次の問いに答えよ。
(1)
0<t≦2のとき、yをtの式で表せ。
(2)
0<t≦8のとき、yとtの関係を表すグラフを下の図にかけ。

(3)
8≦t≦10のとき、t=aで3つの動点P、Q、Rが一直線上に並ぶ。
aの値を求めよ。
@解説@
(1)
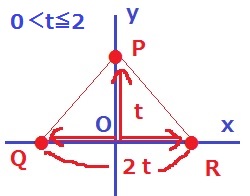
↑2秒後まではこのように広がっていく。
底辺と高さがともに長くなるので、△PQRの面積はy=ax2の形で増加する。
y=2t×t÷2=t2
(2)
2秒ごとに向きが変わるので地道に調べていくしかない。
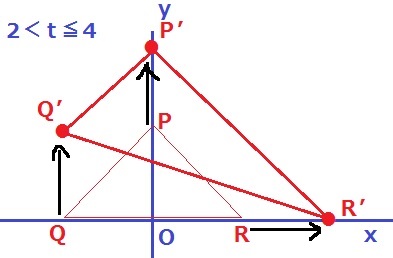
↑移動先をP’、Q’、R’とすると4秒後はこうなる。
PQとP’Q’は平行で長さが等しい。
底辺をP’Q’とすると高さはR’方面となり、
底辺の長さは変わらず、Rが右に離れることで高さだけが長くなる。
ここから△PQRの面積は一次関数で増えていくと考えられる。
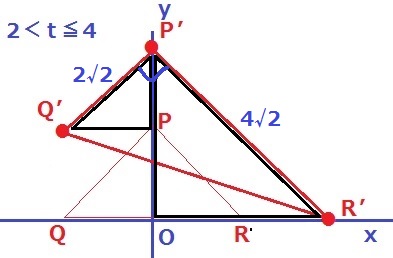
P’Q’とP’R’の傾きが45度である点に注目すると、2つの直角二等辺三角形が見つかる。
P’Q’=2√2、P’R’=4√2、∠R’P’Q’=90°
y=2√2×4√2÷2=8
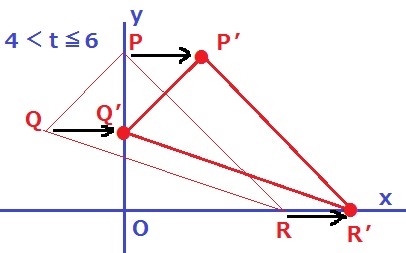
△PQRが平行移動して△P’Q’R’となる。面積は一定。
y=8
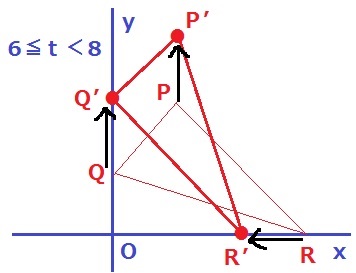
8秒後の様子。
PQ//P’Q’、PQ=P’Q’
底辺をPQとすると、高さはR方向でR→R’のx軸上の移動から高さの成分が減る。
PQ→P’Q’のy軸に対する平行移動から底辺がR’から離れるので、高さの成分が増える。
x軸で高さの減少とy軸で高さの増加が同時に起こる。ここから面積は一定になるのではないかと推測する。

長方形をつくり、周りの3つの三角形を控除する。
y=4×6-2×2÷2-4×4÷2-2×6÷2=8
(*Q’R’の中点が(2、2)なので、4×4÷2=8でもOK)
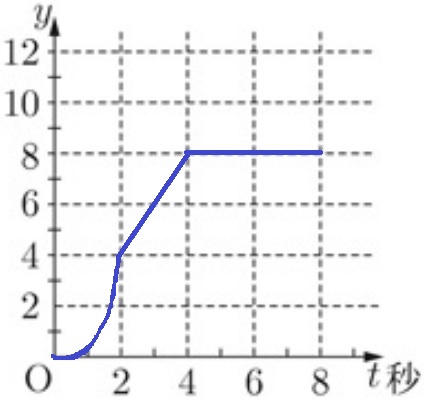
↑解答。途中の変化も問われるので難しい。
(3)
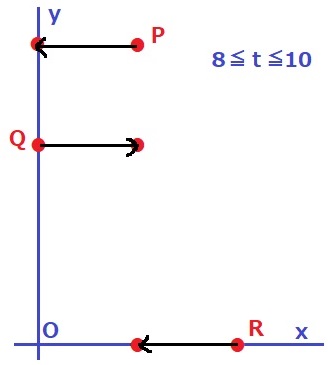
8~10秒後に3点がどう移動するか、正確に描写する。
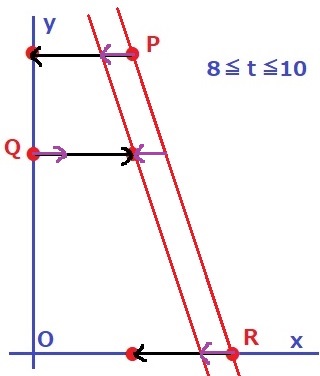
PRに直線を引く。
PとRは同じ速さで同じ方向に移動するので、直線PRは平行移動する。
ということは、Qが直線PR上にくるときを考えればいい。
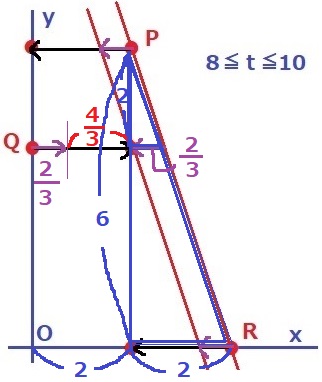
直線PRがQのゴール(2、4)と交わるまでの移動距離を計算する。
青の直角三角形の相似から、2×2/6=2/3
直線PRが(2、4)と交わるとき、同じ速さで動くQも2/3移動している。
残りの距離は、2-2/3=4/3
ここからQと直線PRは1の速さで近づいていく。
出会う時間は、4/3÷2=2/3秒後
したがって、0秒後から計算すると、a=8+2/3+2/3=28/3
@別解@
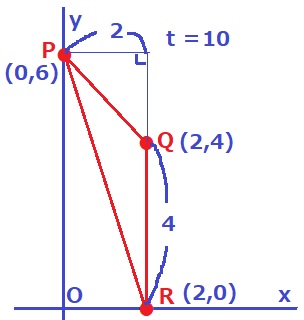
10秒後の様子を考える。
y=4×2÷2=4
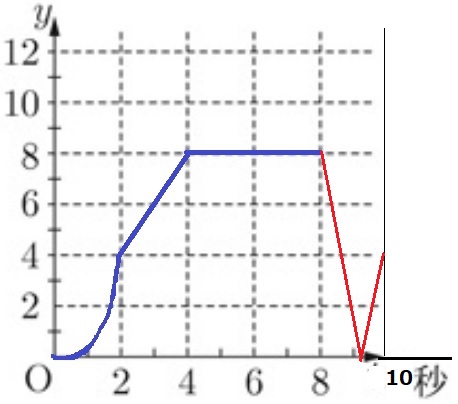
ここで前問のグラフの続きを記入する。
どこかで3点が一直線になると△PQRの面積は0となり、10秒後に4となる。
求めたいのは0となる時間。
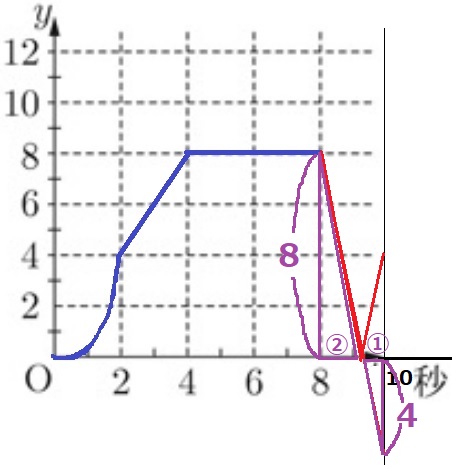
線対称の考えで4を下に移動。
2つの直角三角形の相似を利用する。辺の比は、8:4=②:①
a=8+2×②/③=28/3



コメント