問題ＰＤＦ
下の図のように、ＡＢ＝２√３、ＢＣ＝３である長方形ＡＢＣＤがある。
辺ＡＢの中点をＥとし、辺ＡＤ上に点ＦをＤＦ＝２となるようにとる。
①
ＣＥ、ＥＦ、ＣＦの長さを求めよ。
②
△ＡＥＦ∽△ＥＣＦを証明しなさい。
③
３点Ｃ、Ｄ、Ｆを通る円をＯとしてその中心をＧ、
３点Ｂ、Ｃ、Ｅを通る円をＯ’としてその中心をＨとするとき、ＧＨの長さを求めよ。
④
③のとき、２つの円Ｏ、Ｏ’と長方形ＡＢＣＤのすべてが重なる部分の面積を求めよ。
＠解説＠
①
三平方ですばやく出そう！
ＣＥ…２√３、ＥＦ…２、ＣＦ…４
②
△ＡＥＦ∽△ＥＣＦの証明。
３辺の比がわかっているので、それに着目する。
ＡＥ：ＥＦ：ＦＡ＝ＥＣ：ＣＦ：ＦＥ＝√３：２：１
３辺の比が等しいから∽。
③
円の中心であるＧ・Ｈの位置を特定する。
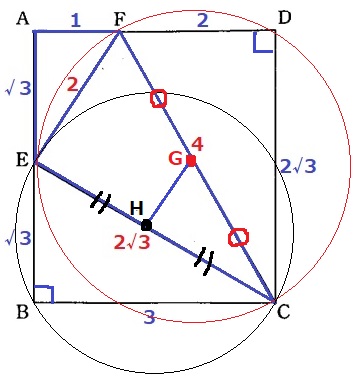
直径に対する円周角は90°！
∠ＣＤＦ＝90°から、円Ｏの中心Ｇは直径ＣＦの中点にある。
∠ＥＢＣ＝90°から、円Ｏ’の中心Ｈは直径ＣＥの中点にある。
さらに、△ＣＧＨと△ＣＦＥにおいて、ＧとＨは各々の辺の中点だから、
中点連結定理により、ＧＨ＝２÷２＝１ｃｍ
④
きっつい:;(∩´＿`∩);:
↑このエリアを求めなさいっちゅーことだが戦意喪失するね！
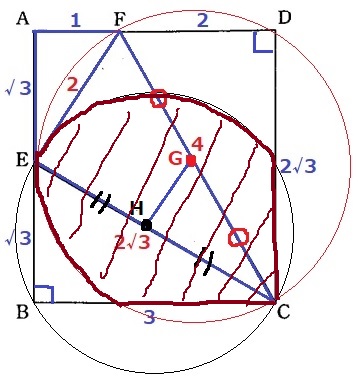
しかし、この問題だけ解説を書かない訳にはいかないので頑張りました。
長さがよくわかっていないので角度の調査。
こういうヘンテコな図形には有名角が隠れているのが定石です|дﾟ)
ＥＣより下と上で分割し、さきに下の部分を求めにいきます。
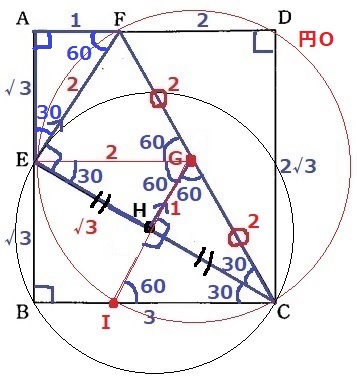
△ＡＥＦは１：２：√３の直角三角形→内角は30°－60°－90°
（２）の△ＡＥＦ∽△ＥＣＦより、△ＥＣＦの内角も30°－60°－90°。
∠ＣＥＦ＝90°だから、Ｅも円Ｏの円周上にある。
ＥＧに補助線。
円Ｏの中心Ｇに注目。
ＦＧ＝４÷２＝２、半径からＥＧ＝２、ＥＦ＝２。
△ＥＦＧは３辺が等しい正三角形。
また、△ＥＧＨは辺の比が１：２：√３→内角が30°－60°－90°の直角三角形！
△ＣＧＨも内角もこれと等しく、ＥＨ＝ＨＣから一辺と両端角相等で△ＥＧＨ≡△ＣＧＨ。
円Ｏと辺ＢＣ上（Ｃ以外）の交点をＩとする。ＧＩに補助線。
∠ＡＥＦ＝30°→∠ＢＥＣ＝60°→△ＢＥＣの残りの内角で∠ＥＣＢ＝30°→∠ＧＣＩ＝60°
半径からＧＩ＝ＧＣ→△ＧＣＩの内角がすべて60°となり正三角形。
（*∠ＩＨＣ＝ＧＨＣ＝90°となり、Ｇ―Ｈ―Ｉは一直線）
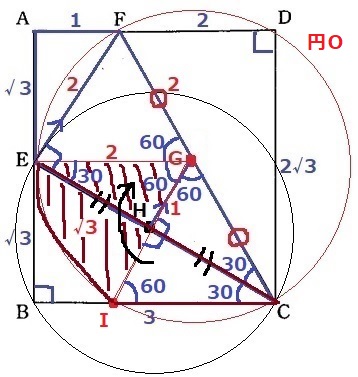
△ＥＧＨと△ＣＩＨは一辺と両端角が等しく合同。
△ＣＩＨを△ＥＧＨに移植すると、半径２ｃｍ中心角60°の扇形になる。
２×２×π×60/360＝２/３πｃｍ2
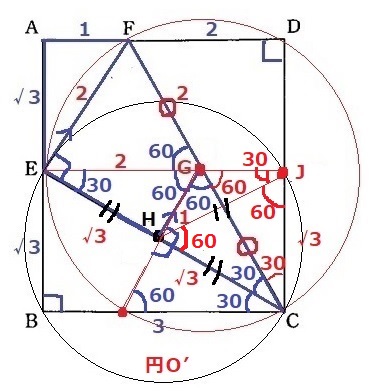
つづいて上の部分にいきます(;´Д｀)ｲﾔ-
円Ｏ’と辺ＣＤ（Ｃ・Ｄ以外）の交点をＪとする。
∠ＧＣＪ＝90－60＝30°
半径から△ＨＪＣは二等辺で、底角の∠ＨＣＪ＝60°だから、
△ＨＪＣの内角はすべて60°で正三角形！
（*ＪＣ＝√３となり、四角形ＥＢＣＪは長方形→Ｅ―Ｇ―Ｊは一直線といえる）
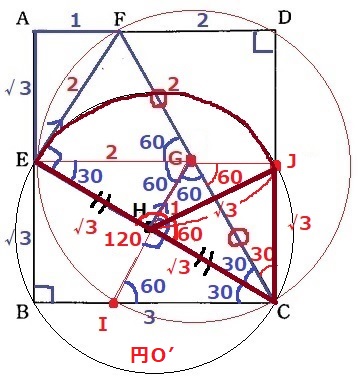
半径√３ｃｍ中心角120°の扇形と、１辺が√３ｃｍの正三角形となる。
正三角形の高さは１：２：√３から、√３×√３/２＝３/２ｃｍ
よって、√３×√３×π×120/360＋√３×３/２×１/２＝π＋３√３/４ｃｍ2
したがって、２/３π＋（π＋３√３/４）
＝５/３π＋３√３/４ｃｍ2
*しんどかった:( ´ω` ):
角度や辺の情報がごちゃごちゃしましたが、途中の説明は他にもいろいろあります。
ポイントは扇形と正方形の交点Ｉ・Ｊがどのような位置にあるのかを見極めることでしょうか。
中心をＧとする円Ｏの弧か、中心をＨとする円Ｏ’の弧か。
いたるところにある１：２：√３の直角三角形を活用する。
鮮やかな解法をついた方は、ぜひ下のコメント欄かお問い合わせよりお知らせ願います<(_ _)>
国私立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント