2020年度　渋谷教育学園幕張高校過去問【数学】大問４解説

問題ＰＤＦ
下の図のように１辺の長さが１の正十二角形があり、６つの頂点をＡ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆとする。

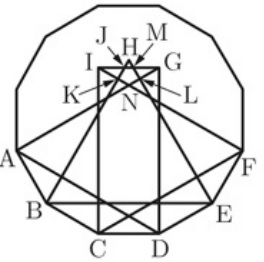
正十二角形の内部に正三角形ＡＤＧ、ＢＥＨ、ＣＦＩをかき、ＩとＧを結ぶ。
ＢＨとＩＧの交点をＪ、ＢＨとＦＩの交点をＫ、ＥＨとＡＧの交点をＬ、
ＥＨとＩＧの交点をＭ、ＡＧとＦＩの交点をＮとする。
このとき、次の各問いに答えなさい。

（１）
ＢＥの長さを求めなさい。

（２）
ＬＧの長さを求めない。

（３）
五角形ＪＫＮＬＭの面積を求めなさい。

（１）

正十二角形の外角は、360÷12＝30°
ＢＥ//ＣＤの錯角と直角で、赤い三角形の内角が30°－60°－90°
→辺の比は１：２：√３
右側も左右対称で同様。ＢＥ＝１×√３/２×２＋１＝√３＋１

（２）
わちゃわちゃした図形で迷子になる:(っ`ω´c):

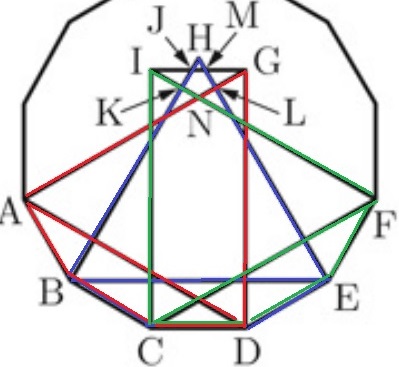
ＡＤ・ＢＥ・ＣＦに注目しよう。
正十二角形の周上で考えると、いずれも頂点２つ飛ばしで長さが等しい。
→ＡＤ＝ＢＥ＝ＣＦ（３つの正三角形は辺の長さが√３＋１で等しい）
また、前問のような１：２：√３の直角三角形が他にもたくさん出てくる。

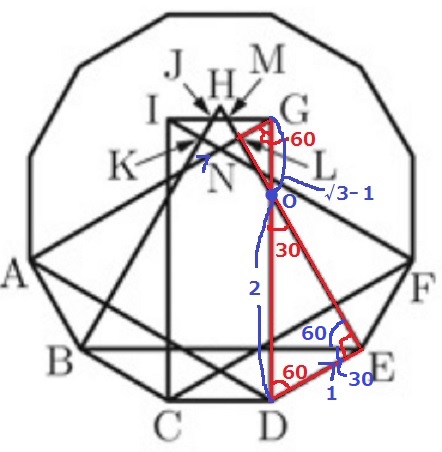
ＬＧを１辺とする三角形に見当をつけよう。
ＨＥとＧＤの交点をＯとする。△ＯＧＬからＬＧの長さを求めたい。

正十二角形の１つの内角は150°。∠ＧＤＥ＝150－90＝60°
正三角形の内角から∠ＤＧＡ＝60°
錯角が等しく、ＡＧ//ＤＥ→△ＯＤＥ∽△ＯＧＬ

∠ＯＥＤ＝30＋60＝90°
△ＯＤＥも△ＯＧＬも辺の比が１：２：√３の直角三角形。
ＯＤ＝１×２＝２
ＧＯ＝ＧＤ－ＯＤ＝（√３＋１）－２＝√３－１
ＬＧ＝（√３－１）×１/２＝（√３－１）/２

（３）
細々とした場所を粘りながら認定していく。
前問のＬＧを使う。

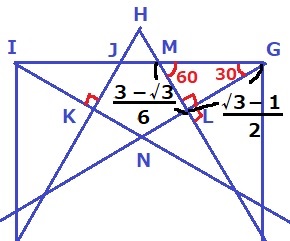
△ＭＧＬも１：２：√３の直角三角形。
ＭＬ＝（√３－１）/２×１/√３＝（３－√３）/６

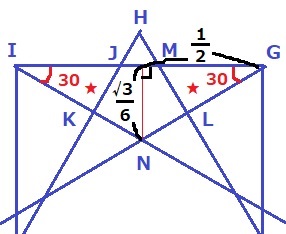
対称性から△ＭＧＬ≡△ＪＩＫ
【△ＩＮＧ－（△ＭＧＬ＋△ＪＩＫ）＝五角形ＪＫＮＬＭ】
△ＩＮＧの内角は30°－30°－120°の二等辺三角形で、
縦半分に割ると１：２：√３の直角三角形。
ＩＧ＝１より、高さは１/２×１/√３＝√３/６

五角形ＪＫＮＬＭの面積は、
１×√３/６÷２－（√３－１）/２×（３－√３）/６÷２×２
＝√３/12－（３√３－３－３＋√３）/12
＝（６－３√３）/12
＝（２－√３）/４
国私立高校入試解説ページに戻る