2023年度　東京学芸大学附属高校過去問【数学】大問４解説

問題ＰＤＦ
∠ＢＡＣ＝90°である直角二等辺三角形ＡＢＣを次の【手順】で折り、図１のように折り目をつける。
ただし、折り目をつけたら、そのたびに元の形に広げる。

ここで、∠ＢＤＨ、∠ＨＤＦ、∠ＦＤＧ、∠ＧＤＩ、∠ＩＤＣの大きさが等しいかどうかについて考える。
【手順】より、∠ＢＤＨ＝∠ＨＤＦ＝∠ＧＤＩ＝∠ＩＤＣが成り立つ。さらに、∠ＢＤＨ＝∠ＦＤＧが成り立つかどうかについて、次の【考察】のようにまとめた。

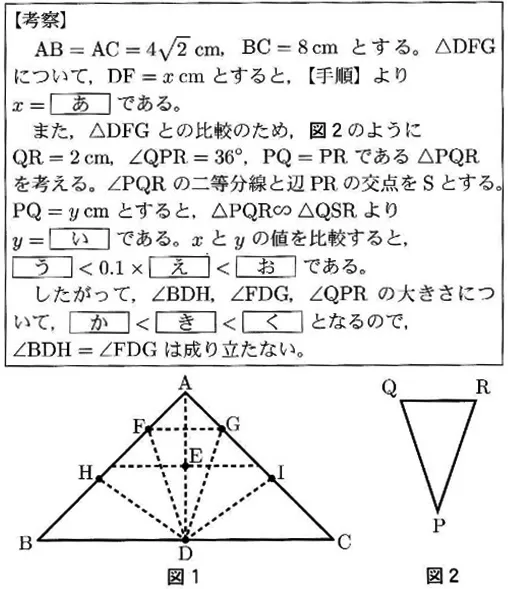
このとき、次の各問いに答えなさい。
（１）
[　あ　]にあてはまる値を求めなさい。

（２）
[　い　]にあてはまる値を求めなさい。

（３）
[　う　]～[　く　]について、次の各問いに答えなさい。
（ⅰ）[　え　]にあてはまる整数を求めなさい。
（ⅱ）[　う　][　お　][　か　][　き　][　く　]にあてはまる組み合わせとして最も適切なものを選びなさい。

＠解説＠
（１）

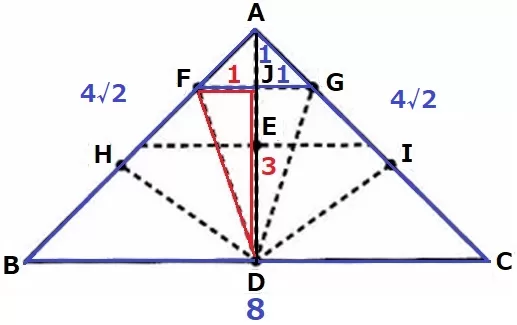
ＤはＢＣの中点、ＥはＡＤの中点。
ＡＤとＦＧの交点をＪとすると、ＪはＡＥの中点。
△ＡＦＧ∽△ＡＢＣの相似比は１：４だからＦＧ＝２ｃｍ→ＦＪ＝１ｃｍ

△ＡＢＤも直角二等辺なので、ＡＤ＝ＢＤ＝４ｃｍ
ＡＪ：ＪＤ＝１：３から、ＪＤ＝３ｃｍ
△ＦＪＤで三平方→ＤＦ＝√10ｃｍ

（２）
ここで別の図形に切り替わる。

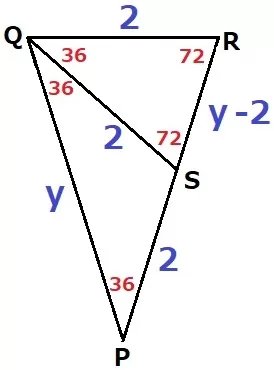
角度を調べると、２角相等で△ＰＱＲ∽△ＱＳＲ
△ＰＱＳも二等辺で、ＱＳ＝ＰＳ＝２ｃｍ
ＳＲ＝ｙ－２ｃｍ
ＰＱ：ＱＲ＝ＱＳ：ＳＲより、ｙ：２＝２：ｙ－２
外項と内項の積から、ｙ（ｙ－２）＝４
ｙ²－２ｙ－４＝０
解の公式より、ｙ＝１±√５
ｙ＞０だから、ｙ＝１＋√５

＠余談＠

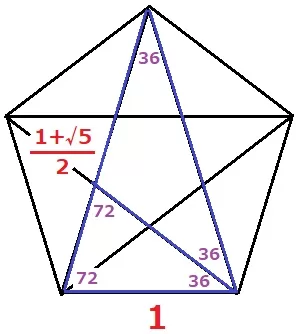
どこかで見かけたことのある人はいたと思う。
正五角形の辺と対角線の比が１：（１＋√５）/２の黄金比になる図。

（３）（ⅰ）

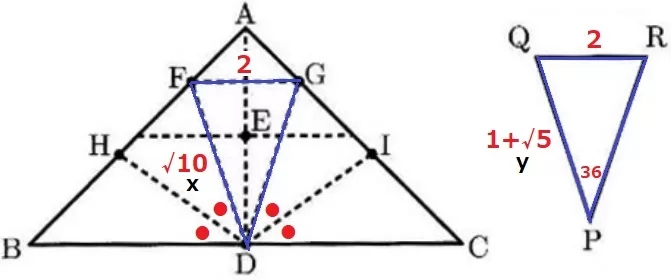
求めたいのは∠ＢＤＨ＝∠ＦＤＧ。
これが成り立つとすると、∠ＦＤＧは180÷５＝36°で∠ＱＰＲと同じになるはず。
そこで、ＦＧ＝ＱＲ＝２ｃｍとなる頂角36°の二等辺三角形ＰＱＲと比較する。

『ｘとｙの値を比較する』の誘導に従う。
√９＜√10＜√16だから、√10は３より上。
√５＝2.2360679（富士山麓オウム泣く）だから、√５＋１≒3.23
…これだけでは比較できないので、√10をもう少し精査する。
3.1²＝9.61
3.2²＝10.24
3.1²＜10＜3.2²ということは、3.1＜√10＜3.2
以上より、√10＜１＋√５となる。

問題文にあてはめると、
√10（ｘ；ＤＦ）＜0.1×（え）＜１＋√５（ｙ；ＰＱ）
√10は3.2未満で１＋√５は3.2を超えるから、（え）＝32

（ⅱ）
角度を比較する。

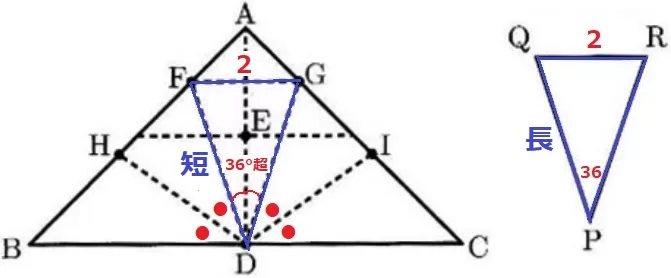
ＤＦ＝短、ＰＱ＝長に置き換える。
底辺の長さが等しい場合、頂角からの距離が短い方があいだの角は大きくなる。
∠ＦＤＧ＞36°
∠ＦＤＧが五等分の36°より大きいということは、残りの４つの角（●）は36°より小さい。
∠ＢＤＨ＜∠ＱＰＲ＜∠ＦＤＧ
イ
国私立高校入試解説ページに戻る