2023年度　都立国立高校過去問【数学】大問４解説

問題ＰＤＦ
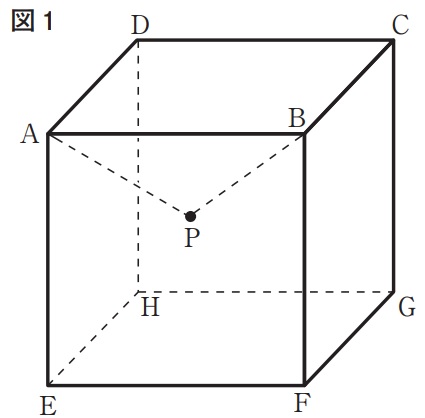
下の図１に示した立体ＡＢＣＤ―ＥＦＧＨは、１辺の長さが３ｃｍの立方体である。点Ｐは、この立方体の内部および全ての面、全ての辺上を動く点である。頂点Ａと点Ｐ、頂点Ｂと点Ｐをそれぞれ結ぶ。ＡＰ＝ａｃｍ、ＢＰ＝ｂｃｍとする。次の各問に答えよ。ただし、円周率はπとする。

〔問１〕
点Ｐがａ＝ｂ＝３を満たしながら動くとき、点Ｐはある曲線上を動く。
点Ｐが動いてできる曲線の長さは何ｃｍか。

〔問２〕
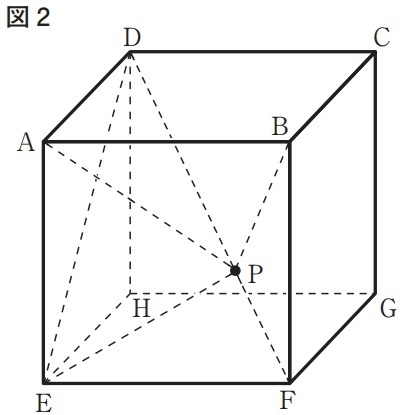
下の図２は、図１において、頂点Ｄと頂点Ｅ、頂点Ｄと頂点Ｆ、頂点Ｅと点Ｐをそれぞれ結び、点Ｐが線分ＤＦ上にある場合を表している。ａ＋ｂの値が最も小さくなるとき、立体Ｐ―ＡＤＥの体積は何ｃｍ³か。ただし、答えだけでなく、答えを求める過程が分かるように、図や途中の式などもかけ。

〔問３〕
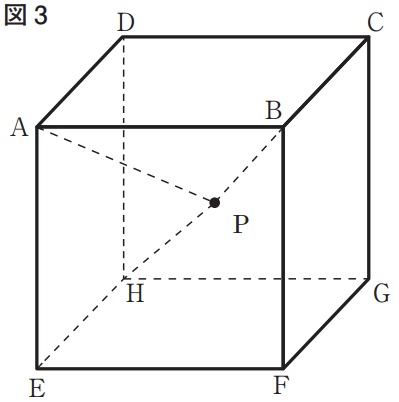
下の図３は、図１において、ａ≧ｂのとき頂点Ｈと点Ｐを結んだ場合を表している。ＨＰ＝ｃｃｍとし、点Ｐがｂ＝ｃを満たしながら動くとき、点Ｐはある多角形の辺上および内部を動く。点Ｐが動いてできる多角形の面積は何ｃｍ²か。

＠解説＠
〔問１〕

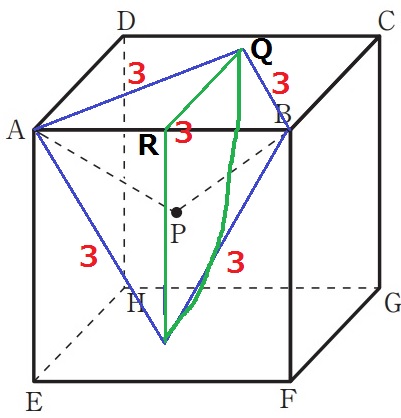
面ＡＢＣＤ上に、辺ＡＢを１辺とする正三角形ＡＢＱをつくる。
この正三角形ＡＢＱをＡＢを軸として面ＡＥＦＢまで回転させるイメージをする。
ＡＢの中点をＲとする。△ＡＲＱは１：２：√３の直角三角形→ＲＱ＝３√３/２

〔問２〕
なんとなくＰはＤＦの中点だと察せるが、説明問題ゆえ逃げられない(´ﾟдﾟ｀)…

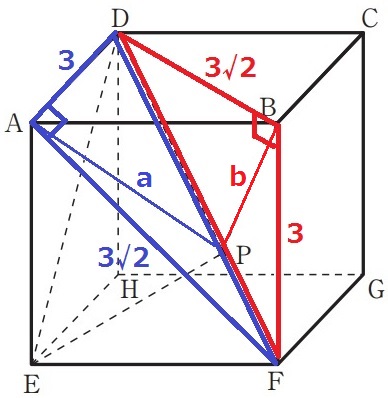
ＰはＤＦ上を動く。
線分ＡＰは△ＡＤＦ上を、線分ＢＰは△ＢＦＤ上を動くことに着目する。
ＡＤ＝ＢＦ＝３ｃｍ、ＡＦ＝ＢＤ＝３√２ｃｍ
ＡＤ⊥面ＡＥＦＢ、ＢＦ⊥面ＡＢＣＤより、∠ＤＡＦ＝∠ＦＢＤ＝90°
２辺とあいだの角が等しく、△ＡＤＦ≡△ＢＦＤ

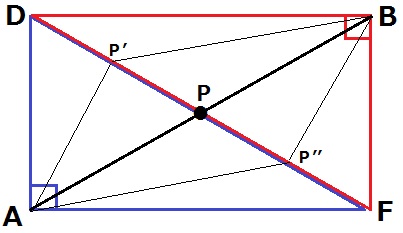
合同な２つの直角三角形を合わせると長方形になる。
ＡＰとＢＰが最短となるのは、ＡＢとＤＦの交点がＰのとき。
長方形の対角線は各々の中点で交わるから、ＰはＤＦの中点である。

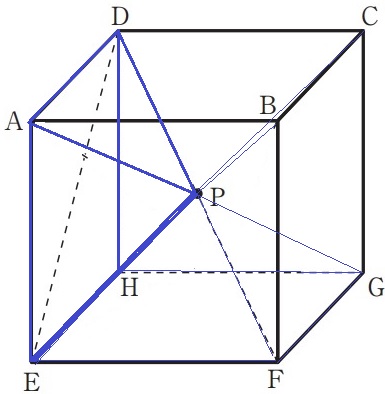
Ｐは立方体の中心である。
四角錐Ｐ―ＡＤＨＥは立方体の６分の１。
（Ｐ―ＡＤＨＥを６つ組み合わせると立方体になる）
三角錐Ｐ―ＡＤＥは底面積が四角錘の半分⇒体積半分なので、
３³÷６÷２＝９/４ｃｍ³

＠＠

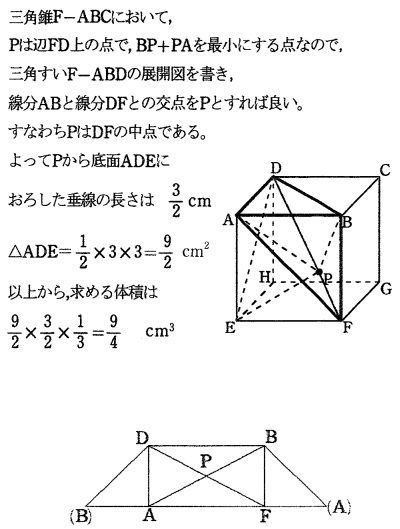
公式解答では三角錐Ｆ―ＡＢＤの展開図から説明しています。

〔問３〕

先にｂ＝ｃを考える。
ＢＰ＝ＨＰということはＰはＢとＨから距離が等しい点の集合で、
これがどうやら多角形になるらしい…。
適当な辺でＰの位置を探るのがやりやすい。
最短距離→展開図の要領で考えると、ＣＤとＣＧの中点が該当する。

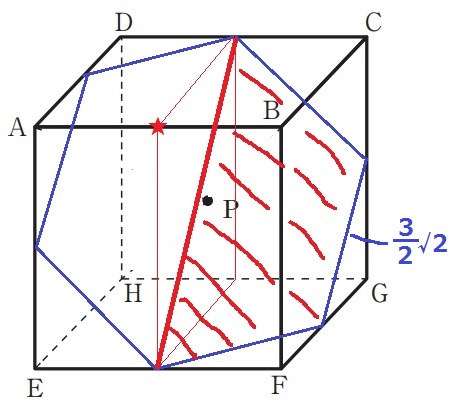
他の辺も調べると、立方体内部でＢとＨから等しい点の集合は正六角形になる。
正六角形の１辺は等辺が３/２ｃｍの直角二等辺の斜辺→３√２/２ｃｍ

次にａ（ＡＰ）≧ｂ（ＢＰ）を考える。
この正六角形のうち、ＡＰ＝ＢＰの場合を含めたＢに近い方の面積を求めたい。
ＡＢの中点★を通り、ＡＢに対して垂直な面が両点からの距離が等しい点の集合である。
この面より右側にある正六角形の半分が答えになる。

求積すべき図形は、１辺が３√２/２ｃｍの正三角形の３個分に相当する。
正三角形の高さは３√６/４ｃｍ。
３√２/２×３√６/４×１/２×３＝27√３/８ｃｍ²

＠余談＠

立方体の辺上において、Ｂから距離が等しい複数の点を動かして考えてみる。
最初はＢＡ、ＢＣ、ＢＦ上の３点で三角錘が拡大していくが、頂点Ａ・Ｃ・Ｆを過ぎると六角形になる。
これをＨ側からもやってみると、Ｂ側の青とＨ側の赤の面が重なるのは正六角形である。

＠余談２＠

ＰはＢとＨから距離の等しい点の集合。
立方体を斜めから見ると、求めるべき多角形は点Ｐを通る線分ＢＨに垂直な線となる。
この線とＤＢ、ＨＦとの交点をそれぞれＩ・Ｊとする。
△ＢＨＦ∽△ＰＨＥ∽ＪＰＥ（２角相等）より、ＢＦ：ＦＨ＝ＪＥ：ＥＰ＝ＰＥ：ＥＨ＝１：√２
比を合わせると、ＨＥ：ＥＪ＝②：①
ＥＦ＝ＨＥ＝②だから、ＪはＥＦの中点である。
対称性からＩもＤＡの中点。
これを立体で捉えなおすと左図のようになり、あとはこれらを通る立方体の切断面を考えばいい。

＠余談３＠

立方体を対角線上（上図はＢ方向から）から眺めると、アウトラインは正六角形になる。
中心のＢ・Ｈから６辺にひいた垂線は、実際の立体でも同じ長さである。
国私立高校入試解説ページに戻る