問題PDF
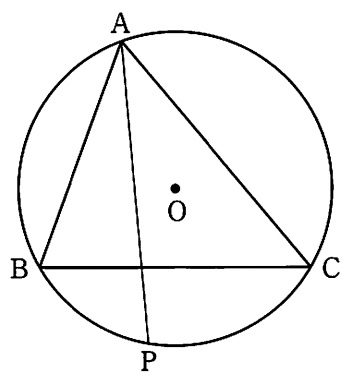
下の図1において、△ABCは鋭角三角形であり、点Oは△ABCの3つの頂点A、B、Cを通る円の中心である。∠Aの二等分線と円Oとの交点のうち、頂点Aと異なる点をPとする。
〔問1〕
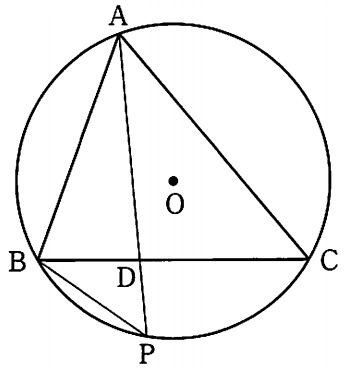
下の図2は、図1において、線分APと線分BCとの交点をDとし、頂点Bと点Pを結んだ場合を表している。AB=6cm、AC=8cm、BD=3cm、BP=4cmであるとき、線分DPの長さは何cmか。
〔問2〕
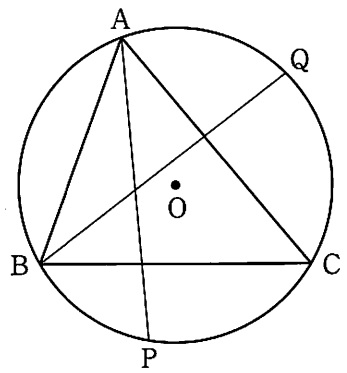
下の図3は、図1において、∠Bの二等分線と円Oとの交点のうち、頂点Bと異なる点をQとした場合を表している。ただし、∠Aの二等分線と∠Bの二等分線は、円の中心Oでは交わらないものとする。
(1)
図3において、頂点Aを含む弧BQに対する円周角の大きさと、頂点Bを含む弧APに対する円周角の大きさが等しくなるとき、△ABCはどのような三角形になるか答えよ。ただし、答えだけでなく、答えを求める過程が分かるように、途中の式や計算なども書け。
(2)
図3において、頂点Aを含む弧BQに対する円周角の大きさと、頂点Cを含む弧APに対する円周角の大きさが等しくなるとき、∠ACBの大きさは何度か。
@解説@
〔問1〕
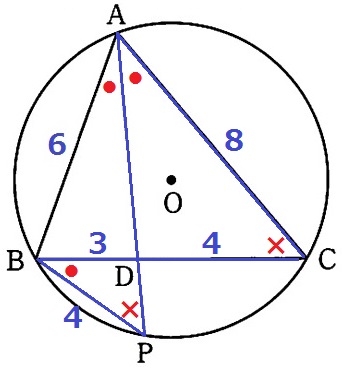
角の二等分線の定理より、AB:AC=BD:DC=3:4
DC=3×4/3=4cm
弧ABに対する円周角より、∠ACB=∠APB
弧PCに対する円周角より、∠PAC=∠PBC
△ACD∽△BPDで、AC:DC=BP:DP=2:1
DP=4÷2=2cm
〔問2〕(1)

円周角が等しい⇒弧BQ(青)と弧AP(赤)の長さが等しい。
共通部分である弧ABをひくと、弧AQ=弧BPが導ける。
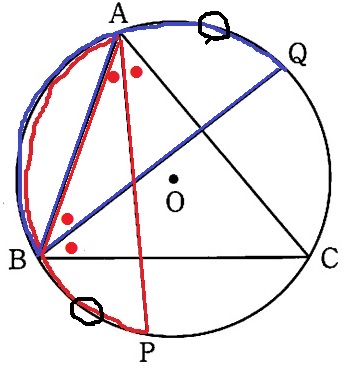
弧の長さが等しいので、∠ABQ=∠BAP(前図の●と×が等しい)
∠CAB=∠CBA(●●)
△ABCは2つの底角が等しいから、CA=CBの二等辺三角形となる。
(2)
弧APが前問と異なる点に注意!
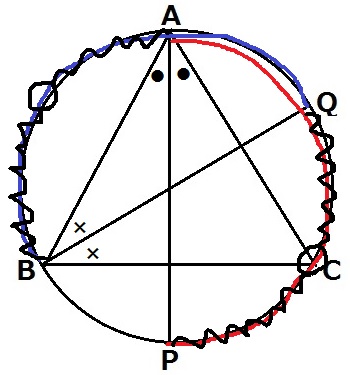
円周角が等しい→弧BQ=弧AP
共通部分の弧AQをひくと、弧AB=弧PQ
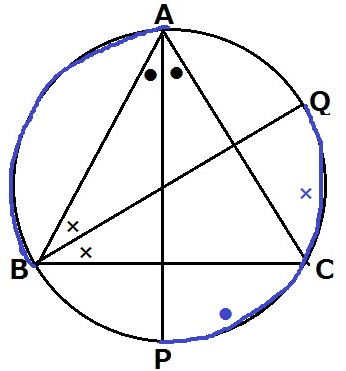
ここで、弧PQを弧PCと弧CQに分けて考える。
弧PCに対する円周角→∠PAC=●
弧CQに対する円周角→∠CBQ=×
弧PQに対する円周角は●+×となる。
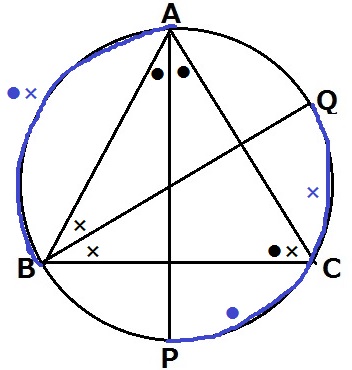
弧AB=弧PQより、弧ABに対する円周角である∠ACB=●+×
△ABCの内角に注目すると、(●+×)×3=180°だから、
∠ACB=●+×=180÷3=60°



コメント