2021年度　岐阜県公立高校入試問題過去問【数学】解説

平均48点（前年比；－１点）

問題はコチラ→ＰＤＦファイル
出題範囲の除外は標本調査。

大問１（小問集合）

（１）　92％
５－３²
＝５－９
＝－４

（２）　82％
６ｘｙ÷２/３ｘ
＝９ｙ

（３）　53％
（ｘ－３）²＝９
ｘ－３＝±３
ｘ＝３±３
ｘ＝０、６

（４）　51％
中央値（メジアン）…11試合の中央値は６番目。２得点
最頻値（モード）…最もあらわれている値。１得点
平均値…（０×１＋１×４＋２×３＋３×２＋４×１）÷11＝20/11≒２未満
エ

（５）　60％
正五角形の１つの内角は、180×（５－２）÷５＝108°
（*もしくは、外角から180－360÷５＝108°でもＯＫ。
108°は頻出なので覚えてしまった方がいい）

正五角形の１辺は等しく、△ＢＣＤは二等辺三角形。
∠ＢＤＣ（●）＝（180－108）÷２＝36°
正五角形の対称性から△ＢＣＤ≡△ＥＤＣで、∠ＥＣＤ（●）＝36°
△ＣＤＦで外角定理→ｘ＝36＋36＝72°

（６）　26％！
水の体積は変わらない。

左は三角錐。
三角錐の体積を立方体の底面積で割ればいい。
９×９÷２×９÷３÷（９×９）
＝３/２ｃｍ

大問２（反比例）

（１）　64％
反比例の比例定数ａは積ｘｙで一定。
ａ＝500×８＝4000
ｙ＝4000/ｘ

（２）　42％
先ほどの式にｘ＝600を代入する。
ｙ＝4000/600＝６・２/３分＝６分40秒

大問３（関数）

（１）　82％
ａは傾き１～６
ｂは切片１～６
先に切片で直線を固定して傾きを変えてみると…重複がない。
直線に条件もない→全部つくれる！
６×６＝36通り

（２）　75％
ａ＝１であれば、ｂは何でもいい。
ａ＝１となる確率は１/６

（３）　９％!!
同じ直線上にない３点を結ぶと三角形ができる。
２つ以上の直線が平行か、３直線が１点で交わると三角形が作れない。

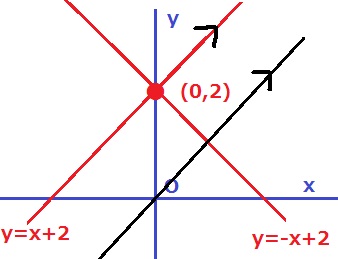
ｙ＝ａｘ＋ｂの傾きａは正の値（１～６）だから右上である。
傾き１、すなわち、ａ＝１のときはｙ＝ｘ＋２との交点がなく、三角形ができない。
ｂ＝１～６の６通り

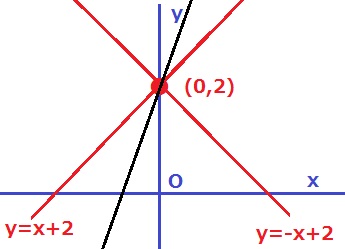
ｙ＝ａｘ＋ｂが（０、２）を通過する、すなわち、ｂ＝２のときも三角形ができない。
ａ＝１～６の６通り
（ａ、ｂ）＝（１、２）の重複を含むので、合計は６＋６－１＝11通り
確率は11/36

大問４（数量変化）

（１）ア…84％、イ…66％
ｘ＝６のとき、ｙ＝５×６＝30

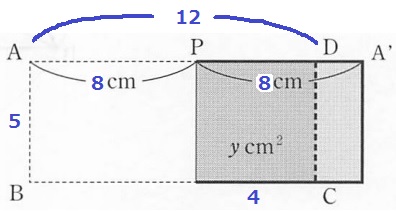
６を超えると重なる部分が減ることに注意！
ｘ＝８のとき、ＰＤ＝12－８＝４
ｙ＝５×４＝20
ア…30、イ…20

（２）ア…71％、イ…52％
０≦ｘ≦６のとき、縦は５、横はｘ。
ｙ＝５ｘ
６≦ｘ≦12のとき、縦は５、横は12－ｘ。
ｙ＝５（12－ｘ）＝－５ｘ＋60
ア…５ｘ、イ…－５ｘ＋60

（３）　72％

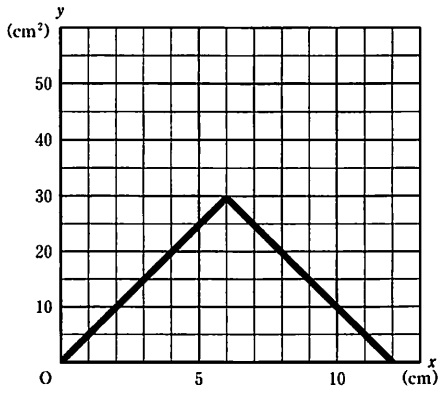
（２）の式をグラフに写す。
ｘ＝６でグラフが折れ、（６、30）（12、０）を通過する。

（４）　６％!!
前問のグラフより、該当する条件はｘが６以下か６以上で２通りある。
ＡＰは左端から折り目までの長さだから、ＡＰを長くするには６≦ｘ≦12のとき。
つまり、Ａ’がＤの右側にくるとき。

重なる部分を②、重ならない部分を①とする。
Ｐより右側にある③を左側に戻す。
ＡＰ：ＡＤ＝③：⑤

ＡＤ＝12ｃｍ
ＡＰ＝12×③/⑤＝7.2ｃｍ

大問５（平面図形）

（１）　59％
ＡＥ＝ＡＤの証明。

△ＡＢＥと△ＡＣＤにおいて、
ＡＢ＝ＡＣ（正三角形の１辺）
ＢＥ＝ＣＤ（仮定）
∠ＡＢＥ＝∠ＡＣＤ（弧ＡＤに対する円周角）
２辺とあいだの角が等しく、△ＡＢＥ≡△ＡＣＤ
対応する辺は等しいから、ＡＥ＝ＡＤ

（２）ア　36％

形はおかしいが…△ＡＢＨに注目すると、
内角が45°－45°－90°の直角二等辺三角形。
辺の比は１：１：√２だから、ＡＨ＝６×１/√２＝３√２ｃｍ

イ　３％!!

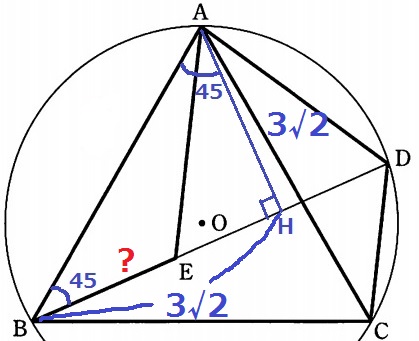
ＢＥを底辺とすると、高さは先ほど求めたＡＨ。
△ＡＢＨは直角二等辺だから、ＢＨ＝ＡＨ＝３√２ｃｍ
ＢＥを求めたいので、ＥＨの長さが知りたい。
・・なんとなく△ＡＤＥが正三角形っぽい。

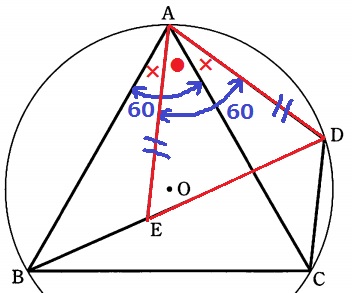
（１）の合同を利用する。
∠ＢＡＣ＝●＋×＝60°
合同の対応する角で∠ＣＡＤ＝∠ＢＡＥ＝×だから、∠ＥＡＤ＝●＋×＝60°
ＡＥ＝ＡＤ
△ＡＥＤは頂角ＥＡＤ＝60°の二等辺三角形⇒△ＡＥＤはやはり正三角形

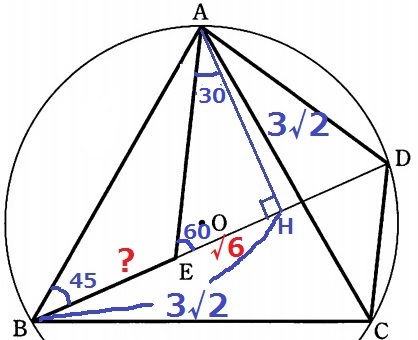
△ＡＨＥは正三角形ＡＤＥの半分→内角は30°－60°－90°→辺の比は１：２：√３
ＥＨ＝３√２×１/√３＝√６ｃｍ
ＢＥ＝３√２－√６ｃｍ
△ＡＢＥの面積は、（３√２－√６）×３√２÷２
＝（18－６√３）÷２＝９－３√３ｃｍ²

大問６（整数）

（１）　54％

正の平方根の整数部分が変わるタイミングは、表が平方数であるとき。
√９（３）＜√10＜√16（４）
√10の整数部分は３。

（２）ア…47％、イ…22％！、ウ…26％！、エ…16％！、オ…16％！
√144（12）＜√150＜√169（13）
表が150のカードの裏は12。

◆ｎ＝12のとき
裏が12のカードは144～150。
150－144＋１＝７枚
（*＋１を忘れないこと！）

◆ｎ＜12のとき
裏がｎのカードは、表がｎ²から（ｎ＋１）²の１個手前までフルにある。
最も小さい表の数はｎ²
最も大きい表の数は、（ｎ＋１）²－１＝ｎ²＋２ｎ

裏がｎのカードの枚数＝表がｎ²～ｎ²＋２ｎの枚数。
（ｎ²＋２ｎ）－ｎ²＋１＝２ｎ＋１枚
（*＋１を忘れないこと！）
ア…12、イ…７、ウ…ｎ²、エ…ｎ²＋２ｎ、オ…２ｎ＋１

（３）　34％
前問の２ｎ＋１にｎ＝９を代入。
２×９＋１＝19枚
（*81～99までの19枚。（２）オがわからなかったとしてもチャレンジしたい）

（４）　１％!!!
150枚の裏の数を全てかけ合わせた数Ｐを３^ｍで割ると整数になる。
⇒Ｐを÷３÷３÷３…とｍ回割り続けて割り切れる。
ｍを最も大きくするので、言い換えれば、Ｐに３の素因数が何個含まれるかを数えればいい。
２ｎ＋１のｎに３の倍数を代入する。

◆表が３のカード
２×３＋１＝７枚
◆表が６のカード
２×６＋１＝13枚
◆表が９のカード
２×９＋１＝19枚
◆表が12のカード
（２）イより７枚だけ。

注意点は、９は素因数３が２つずつあること！（９＝３×３）
９のカードの枚数は２倍する。
ｍ＝７＋13＋19×２+７＝65