2021年度　奈良県公立高校入試問題過去問【数学】解説

平均27.6点（前年比；＋2.2点）

問題はコチラ→ＰＤＦファイル
出題範囲の縮小は標本調査。

大問１（小問集合）－72.4％

（１）①　98.3％
－２－５
＝－７

②　95.4％
－３²×９
＝－９×９
＝－81

③　81.7％
８ａ²ｂ÷（－２ａｂ）²×６ａｂ
＝８ａ²ｂ÷４ａ²ｂ²×６ａｂ
＝12ａ

④　79.5％
（ｘ＋７）（ｘ－４）－（ｘ－４）²　←共通因数（ｘ－４）でくくる
＝（ｘ－４）{（ｘ＋７）－（ｘ－４）}
＝11（ｘ－４）
＝11ｘ－44

（２）　93.0％
３ｘ＋４ｙ＝１
２ｘ－ｙ＝－３
加減法がやりやすいかな？
ｘ＝－１、ｙ＝１

（３）　86.7％
ｘ²－３ｘ＋１＝０
解の方式を適用して、ｘ＝（３±√５）/２

（４）　50.4％
√９＜√15＜√16
⇒√15の整数部分は３。
√15の小数部分は√15－３。

ａ²＋６ａ
＝ａ（ａ＋６）　←代入
＝（√15－３）（√15＋３）
＝15－９＝６

（５）　62.4％
ア：Ａ…５/30、Ｂ…５/73
分数で比較すると、分子が同じなので分母の小さいＡが大きい。〇
イ：Ａ…５人、Ｂ…５人×
ウ：Ａ…7.5時間、Ｂ…7.5時間×
エ：Ｂの７時間未満は37人。37×２＝74だから、37/73は半分を超える。〇
ア・エ

（６）　70.3％

立方体の対角線上にある２点は、展開図では２つ分の長方形の対角線上にある。
ウ

（７）　60.7％
正三角形をつくり、60°を二等分すれば30°ができる。

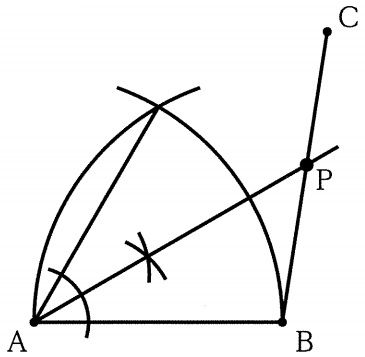
①線分ＢＣをひく。
②ＡＢの長さをとって正三角形を作成。
③60°を二等分。ＢＣとの交点がＰとなる。

（８）①　77.8％
最も小さい数をａとすると、連続する４つの整数はａ、ａ＋１、ａ＋２、ａ＋３。
最も大きい数はａ＋３。

②　53.9％
2021÷３＝673…２
2021は３の倍数ではない。

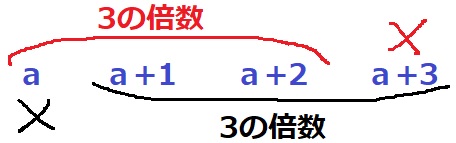
連続する３つの整数の和は３の倍数（均すと真ん中の数になる）
ａかａ＋３を除外すると、残りの和は必ず３の倍数になる。
ということは、除外するのはａ＋１かａ＋２のどちらか。

ａ＋１を除外すると３ａ＋５
ａ＋２を除外すると３ａ＋４

2021＝673×３＋２＝672×３＋５
ａ＋（ａ＋２）＋（ａ＋３）＝３ａ＋５

＋５が共通する→除外するのはａ＋１
３ａ＝672×３
ａ＝672
ａ＋１＝673

大問２（文字式）－49.6％

（１）①あ…84.4％、い…57.5％
活用の問題。きちんと情報整理すること！
花子のグループは特別割引の適用を受ける。
大人２人だから、子供２人分が無料になる。
500×２＋200×１＝1200円

太郎のグループが特別割引の適用を受けた場合、
500×３＋200×２＝1900円
月末割引の場合は大人１人が450円、子供１人が150円になる。
450×３＋150×５＝2100円
差額は200円。
あ…1200、い…200

②　44.2％
特別割引では子供料金が大人の人数分タダになる。
ｘ＜ｙのとき、子供料金はｙ－ｘ人分。

大人の料金…500ｘ円
子供の料金…200（ｙ－ｘ）円
500ｘ＋200（ｙ－ｘ）
＝300ｘ＋200ｙ
（*ｘ＞ｙのときは子供料金がゼロ。すなわち、500ｘ円になる）

③う…49.6％、記号…62.4％
特別割引は前問の300ｘ＋200ｙ円
月末割引は450ｘ＋150ｙ円

これらが等しくなるので、
300ｘ＋200ｙ＝450ｘ＋150ｙ
150ｘ＝50ｙ
３ｘ＝ｙ

ｘ：ｙ＝１：３のときに等式が成り立つ。
→子供の人数ｙが大人の人数ｘの３倍のとき。

後半は、月末料金が安くなる場合（＝特別割引が高くなる場合）を考える。
大人１人増えると、特別割引では大人が＋500円、子供が－200円、トータルで＋300円。
月末割引では＋450円。
→大人の人数が増えるほど特別割引の方が安くなる。
＝大人の人数が減るほど月末料金の方が安くなる。

子供１人増えると、特別割引では＋200円、月末料金では＋150円。
子供の人数が増えるほど、月末料金の方が安くなる。
う…３、ウ

（２）　21.0％！
Ａは１つ、Ｂは２つ。
【少なくとも１人はＡを選ぶ＝全体－３人ともＢを選ぶ】
１－２/３×２/３×２/３
＝19/27

大問３（関数）－52.7％

（１）①　80.9％
ａの値が大きくなるほど、グラフの開きは小さくなる。
イ

②　54.8％
グラフの開きが小さくなるほどｘ軸方向は短くなるが、ｙ軸方向は長くなる！
極端なケースを考えてみるとわかりやすい。
ａ＝１のとき、Ａ（－１、１）Ｂ（２、４）
ａ＝1000のとき、Ａ（－１、1000）Ｂ（２、4000）
ＡＢの長さは後者が圧倒的に長い。傾きが大きくなるほど長くなる。
ア

（２）　75.7％
ａ＞０は下に凸のグラフ。
ｘ＝２のとき、最大値ｙ＝２
（２、２）を通る。

ｙ＝ａｘ²に代入。
２＝４ａ
ａ＝１/２

（３）①　77.4％
ｙ＝２ｘ²に代入。
Ａ（－１、２）⇒Ｂ（２、８）
右に３、上に６だから傾きは２。
Ａから右に１、上に２移動して切片は４。
ｙ＝２ｘ＋４

②　10.7％！

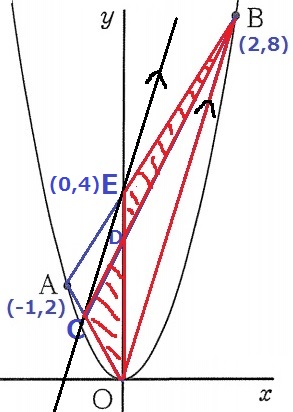
△ＢＥＤと△ＯＣＤの面積が等しい⇒この手のタイプは他の部分を巻き込んでみる。
各々の三角形に△ＢＤＯを足すと、△ＢＥＯと△ＢＣＯの面積が等しいことになる。
等積変形により、ＣＥ//ＯＢ

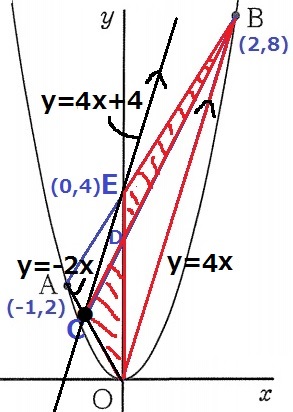
ＯＢの傾きは４。
Ｅ座標は前問の式の切片で（０、４）
ＣＥの式は、ｙ＝４ｘ＋４
ＡＯの式は、ｙ＝－２ｘ

Ｃはｙ＝４ｘ＋４とｙ＝－２ｘの交点だから、
４ｘ＋４＝－２ｘ
ｘ＝－２/３

大問４（平面図形）－30.1％

（１）　74.6％
△ＡＣＤ∽△ＥＢＤの証明。

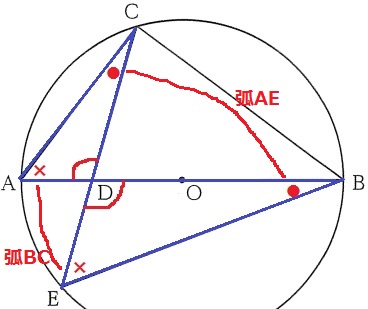
円周角の定理と対頂角で２角相等→∽

（２）　41.5％

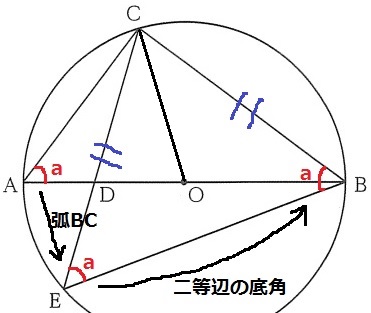
弧ＢＣに対する円周角と二等辺の底角で∠ａを移動させる。
求めたいのは∠ＯＣＤの大きさ。ここからどうつなげるか。

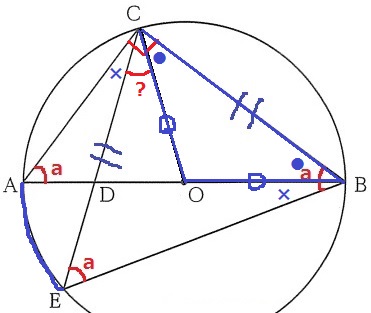
ポイントは、∠ＣＢＥを２つの角（●と×）に分けること！
半径よりＯＢ＝ＯＣ、△ＯＢＣは二等辺で∠ＯＣＢ＝●
弧ＡＥに対する円周角より、∠ＡＣＥ＝×
半円の弧に対する円周角より、∠ＡＣＢ＝90°
したがって、∠ＯＣＤ＝90－（●＋×）＝90－ａ°

（３）　8.1％！

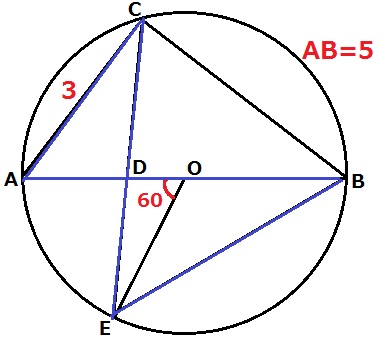
ＡＤとＤＥの長さの比が知りたい。
ＡＤとＤＥそれぞれを１辺とする三角形の相似を探す。
→（１）△ＡＣＤ∽△ＥＢＤを活用する。

ＡＣに対応する辺はＥＢ。
有名角の60°を使ってＥＢの長さを求める。

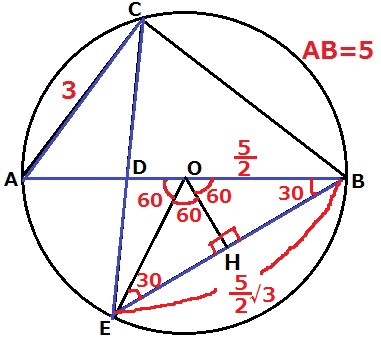
∠ＢＯＥ＝180－60＝120°
半径より△ＯＢＥは二等辺三角形で、内角は120°－30°－30°
これをＯからＢＥに垂線ＯＨをひいて二等分すると有名三角形があらわれる。

ＯＢ＝５÷２＝５/２ｃｍ
直角三角形ＯＢＨの辺の比は１：２：√３でＨはＥＢの中点だから、
ＥＢ＝５/２×√３/２×２＝５√３/２ｃｍ

△ＡＣＤ∽△ＥＢＤで、ＡＣ：ＥＢ＝ＡＤ：ＥＤ
＝３：５√３/２＝６：５√３＝１：５√３/６
（*『ＡＤの長さの何倍か』だから基準となるＡＤを１にする）
よって、ＤＥの長さはＡＤの長さの５√３/６倍。

（４）　0.2％!!!

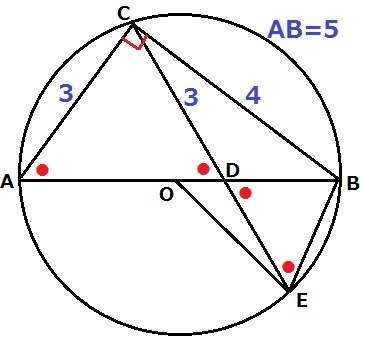
ＡＣ＝ＣＤとなるように図を描きなおす。
対頂角と弧ＢＣの円周角で等角（●）を移動させると、△ＢＤＥも二等辺三角形。
△ＡＢＣは辺の比が３：４：５の直角三角形ゆえ、ＢＣ＝４ｃｍ

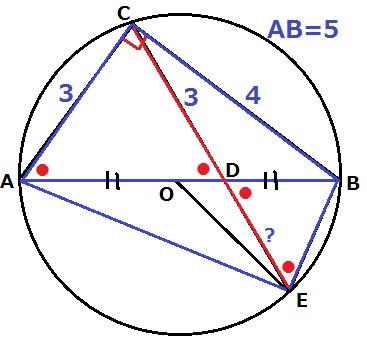
求積したいのは△ＯＥＢだが、これと相似関係にある三角形が見当たらない。。
ここで、ＡＥに補助線をひく。
ＯはＡＢの中点だから、△ＯＥＢの面積は△ＡＥＢの半分である。
また、△ＡＣＢと△ＡＥＢは底辺がＡＢで共通しており、高さの比はＣＤ：ＤＥにあたる。
△ＡＣＢの面積は、３×４÷２＝６ｃｍ²
ＣＤ＝３ｃｍもわかっている。
ＤＥの長ささえわかれば、△ＡＣＢ：△ＡＥＢ＝ＣＤ：ＤＥを利用して
△ＡＥＢの面積が求まり、それを半分にすれば△ＯＥＢの面積になる。
ＤＥの長さを知りたいが、下半分の情報が乏しい…。

ポイントは３：４：５の直角三角形の相似。
ＣからＡＢに垂線ＣＨを引くと、△ＣＨＡも３：４：５の直角三角形。
ＣＡ＝⑤とすると、ＡＨ＝③
△ＡＣＤは二等辺三角形で、ＣＨを対称の軸とするとＤＨ＝ＡＨ＝③
ＡＤ＝３×⑥/⑤＝18/５ｃｍ
ＤＢ＝５－18/５＝７/５ｃｍ

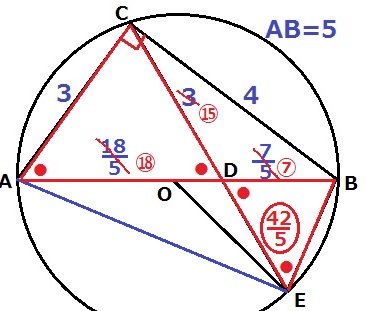
いったん比を整理する。
ＣＤ：ＡＤ：ＤＢ
＝３：18/５：７/５
＝⑮：⑱：⑦
△ＡＣＤ∽△ＥＢＤより、ＤＥ＝⑱×⑦/⑮＝〇42/５

ＣＤ：ＤＥ＝⑮：〇42/５＝75：42＝25：14
したがって、△ＯＥＢの面積は、６×14/25×１/２＝42/25ｃｍ²