2021年度　福島県公立高校入試問題過去問【数学】解説

平均24.2点（前年比；＋2.4点）

問題はコチラ→ＰＤＦファイル
出題範囲の縮小は標本調査。

大問１（計算）

（１）①　99.1％
３×（－８）
＝－24

②　84.3％（部分正答8.7％）
１/２－５/６
＝－１/３

③　87.1％
－８ｘ³÷４ｘ²×（－ｘ）
＝２ｘ²

④　90.6％
√50＋√２
＝５√２＋√２
＝６√２

（２）　79.8％
ｎ角形の内角の和→180（ｎ－２）
180（６－２）＝720°

大問２（小問集合）

（１）　68.6％
√２＝1.41421356…（ 一夜一夜に人見ごろ）
－２√２＝－２×1.414…＝－2.828…
－３＜－２√２

（２）　75.0％
126×２/７
＝36人

（３）　41.9％（部分正答0.3％）
花屋から駅までの600ｍを毎分60ｍで歩く。
600÷60＝10分

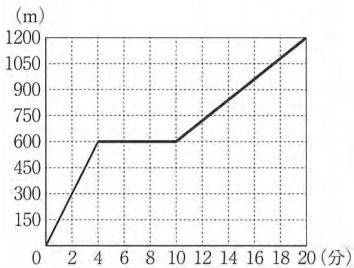
（20、1200）から遡さかのぼる。
20分の10分前に花屋を出発する⇒（10、600）
これらを結ぶ。花屋には６分間、滞在していたことになる。

（４）　43.3％（部分正答0.2％）
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
ａ（２＋６）＝－４
ａ＝－１/２

（５）　92.7％

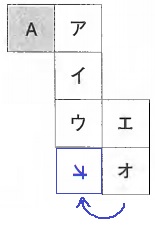
イを底面にして組み立てるとわかりやすい。
もしくは、上図のようにオを90°回転させるとアイウオが一列になるから、
これらが側面となり、Ａとエが平行。
エ

大問３（確率・データの活用）

（１）①　71.2％
Ｄに止まるには２ａ＋ｂの値が３・８・13…になればいい。
◆２ａ＋ｂ＝３
（ａ、ｂ）＝（１、１）だが、ｂに１がない！×
◆２ａ＋ｂ＝８
（２、４）（３、２）
◆２ａ＋ｂ＝13
（４、５）
◆２ａ＋ｂ＝18
最大で２×４＋５＝13だから、もう無い。
３通り

②　14.7％！（部分正答5.1％）
なんとか全部を調べずに済む方法はないか。。

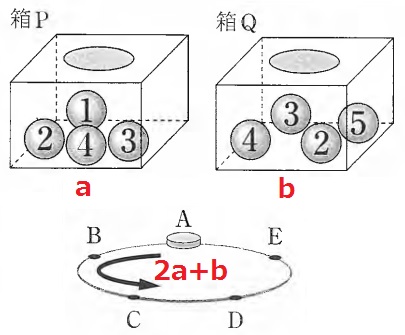
先にａを決める。
ａ＝１、２、３、４のとき、コインは順にＣ、Ｅ、Ｂ、Ｄに止まる。

ここからｂの分だけ反時計回りにコインを動かす。
ｂは２～５だから、１個先以外にコインが止まる。
ＣだったらＤ以外、ＥだったらＡ以外、ＢだったらＣ以外、ＤだったらＥ以外に止まる。
…ということは、Ｂに最も止まる。

Ｂに止まるには、２ａ＋ｂの値が１、６、11、16…
◆２ａ＋ｂ＝１
無い。
◆２ａ＋ｂ＝６
（ａ、ｂ）＝（１、４）（２、２）
◆２ａ＋ｂ＝11
（ａ、ｂ）＝（３、５）（４、３）
◆２ａ＋ｂ＝16
これ以上は無い。
計４通り。確率は４/16＝１/４

（２）①　64.2％
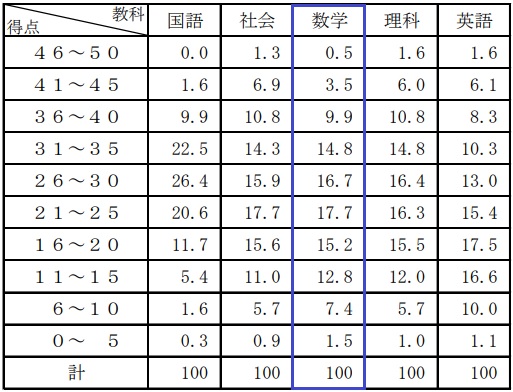
範囲（レンジ）＝最大値－最小値
46－（最小値）＝31
最小値は15ｍ。

②　49.6％（部分正答20.9％）
答案では理由も記述するが、階級を示して比較すれば足りる。
25回の中央値（メジアン）は、（25＋１）÷２＝13番目
中央値が含まれる階級はＡが25ｍ以上30ｍ未満、Ｂが30ｍ以上35ｍ未満。
Ｂの方が大きい。

大問４（整数）

19.4％！（部分正答24.1％）
答案では過程も記述する。
途中で百の位と一の位をチェンジする。
百の位をｘ、一の位をｙとすると、十の位はｘ－２。

位の和が18だから、
ｘ＋（ｘ－２）＋ｙ＝18
２ｘ＋ｙ＝20　…①

百の位と一の位をチェンジして、
｛100ｘ＋10（ｘ－２）＋ｙ｝－｛100ｙ＋10（ｘ－２）＋ｘ｝
＝99ｘ－99ｙ
＝99（ｘ－ｙ）＝99
ｘ－ｙ＝１　…②

①と②の連立を解くと、ｘ＝７、ｙ＝６
十の位は７－２＝５
はじめの自然数は756。

大問５（平面図形）

18.7％！（部分正答24.8％）
ＡＦ＝ＤＧの証明。

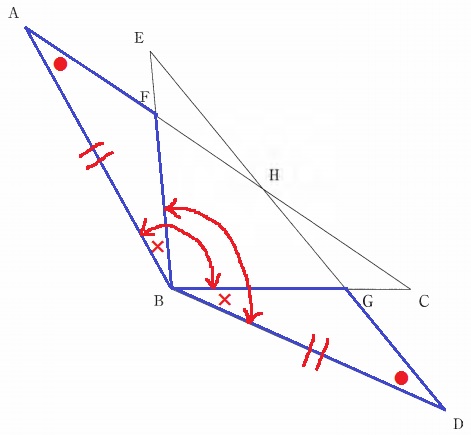
方針は立てやすい。
ＡＦを１辺とする△ＡＢＦ、ＤＧを１辺とする△ＤＢＧの合同を指摘する。

仮定より、ＡＢ＝ＤＢ　…①
仮定より、∠ＢＡＦ＝∠ＢＤＧ（●）　…②
仮定より、∠ＡＢＣ＝∠ＤＢＥ
あいだの角である∠ＣＢＥをひいて、∠ＡＢＦ＝∠ＤＢＧ（×）　…③
①、②、③より、１辺と両端角が等しく、△ＡＢＦ≡△ＤＢＧ
対応する辺は等しく、ＡＦ＝ＤＧ

＠別解＠

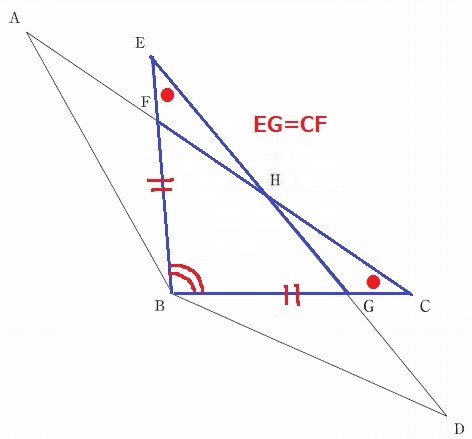
公式解答の２つ目は、１辺両端角相等で△ＥＢＧ≡△ＣＢＦを指摘する。
対応する辺でＥＧ＝ＣＦ
△ＡＢＣ≡△ＤＢＥの対応する辺でＡＣ＝ＤＥ
ＡＦ＝ＡＣ－ＣＦ、ＤＧ＝ＤＥ－ＥＧから、ＡＦ＝ＤＧを導く。

大問６（関数）

（１）　67.2％
Ｐはｙ＝１/２ｘ＋４とｙ＝－１/２ｘ＋２の交点。
１/２ｘ＋４＝－１/２ｘ＋２
ｘ＝－２

ｙ＝１/２ｘ＋４にｘ＝－２を代入。
ｙ＝１/２×（－２）＋４＝３
Ｐ（－２、３）

（２）①　45.4％（部分正答0.5％）

ｙ＝１/２ｘ＋４にｙ＝６を代入。
Ｒ（４、６）
ｙ＝－１/２ｘ＋２にｙ＝６を代入。
Ｓ（－８、６）
△ＰＲＳの底辺ＳＲは４－（－８）＝12、高さは６－３＝３
面積は12×３÷２＝18

②　4.7％!!（部分正答0.2％）

ＡとＢのｙ座標はそれぞれの式の切片。
△ＡＢＰの面積は、２×２÷２＝２
△ＰＲＳの面積は、２×５＝10になればいい。

ここで、前問の△ＰＲＳの底辺12、高さ３に着目する。
ｔはＱのｙ座標。
ｔの値を変えるとＳＲが上下に平行移動する。

ということは、底辺と高さの比は相似で変わらない。
Ｐから垂線、ＳＲの交点をＴとおく。
ＴＰ：ＳＲ＝３：12＝①：④
ＴＰをｘとすると、ＳＲは４ｘ。

４ｘ×ｘ÷２
＝２ｘ²＝10
ｘ＞０だから、ｘ＝√５
求めたいｔは、Ｐのｙ座標にＴＰを足せばいい。
ｔ＝３＋√５

大問７（空間図形）

（１）　67.2％
△ＡＢＣは等辺２ｃｍの直角二等辺三角形。
辺の比は１：１：√２→ＡＣ＝２√２ｃｍ
仮定より、ＡＥ＝ＡＣ＝２√２ｃｍ

（２）　48.2％

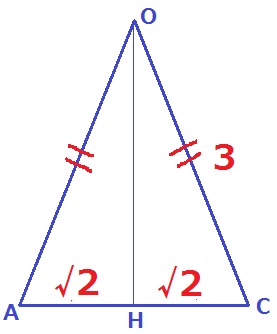
△ＯＡＣは二等辺三角形。
Ｏから垂線、足をＨとする。ＨはＡＣの中点である。
△ＯＨＣで三平方→ＯＨ＝√７
△ＯＡＣの面積は、２√２×√７÷２＝√14ｃｍ²

（３）　1.2％!!
前問の△ＯＡＣ＝√14ｃｍ²を利用できないものか。

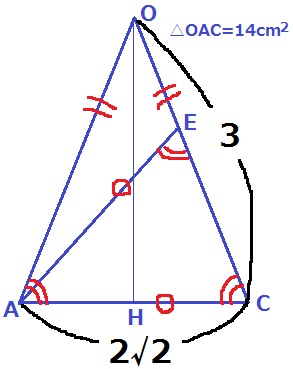
∠ＯＣＡが共通角であることに注目して、
２つの二等辺三角形は２角相等で相似⇒△ＯＡＣ∽△ＡＥＣ
相似比はＯＣ：ＡＣ＝３：２√２
面積比は相似比の２乗なので、△ＯＡＣ：△ＡＥＣ＝９：８
△ＡＥＣ＝√14×８/９＝８√14/９ｃｍ²

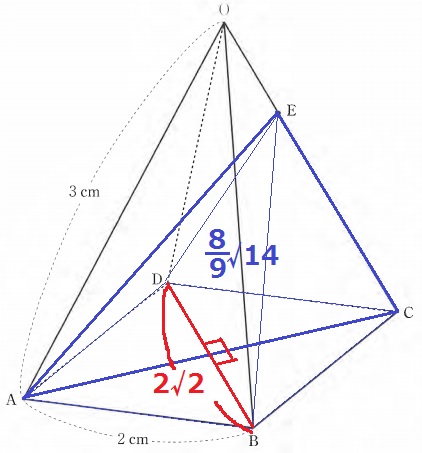
四角錘Ｅ―ＡＢＣＤは面ＡＥＣを境に左右対称。
△ＡＥＣを底辺とすると高さの合計は最大幅であるＢＤ＝２√２ｃｍである。
８√14/９×２√２÷３＝32√７/27ｃｍ³