2022年度　青森県公立高校入試問題過去問【数学】解説

平均53.1点（前年比；－3.1点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）ア　97.4％
－５＋７
＝２

イ　56.3％
（－0.4）×３/10
＝－２/５×３/10
＝－３/25
*（－0.4）×0.3＝－0.12でも良い。

ウ　61.8％
１/３ｘ＋ｙ－２ｘ＋１/２ｙ
＝－５/３ｘ＋３/２ｙ

エ　84.7％
24ａｂ²÷（－６ａ）÷（－２ｂ）
＝２ｂ

オ　78.7％
（√５－√２）（√２＋√５）
＝（√５－√２）（√５＋√２）
＝（√５）²－（√２）²
＝５－２
＝３

（２）　47.5％
９×９×π×60/360
＝27/２πｃｍ²
*約分が適切でない誤答が多かった。

（３）　64.2％
絶対値が最も大きい数⇒数直線上で原点０から最も離れる数。
わかりやすいように【2.7、７/３、３、√６】とすべて正の数に置き換える。
７/３＝2.33…
【2.7と７/３と３】のなかでは、３が最も大きい。

√４＜√６＜√９
２＜√６＜３
√６は３未満。
原点０から最も離れるのは３なので、答えは－３。

（４）連立方程式…57.6％、個数…56.0％
いろいろ設定されているので立式しやすい。
ドーナツがｘ個、クッキーがｙ個。
小麦粉で等式⇒26ｘ＋８ｙ＝380　…①
バターで等式⇒1.5ｘ＋４ｙ＝75　…②
①－②×２をすると、23ｘ＝230
ｘ＝10
②に代入して、ｙ＝15
ドーナツ…10個、クッキー…15個

（５）　46.2％
ｙの変域が０以下なので、ｙ＝ａｘ²は上に凸のグラフ。
ｘ＝３のとき、最小値ｙ＝－６
ｙ＝ａｘ²に（ｘ、ｙ）＝（３、－６）を代入。
－６＝９ａ
ａ＝－２/３

（６）　61.1％

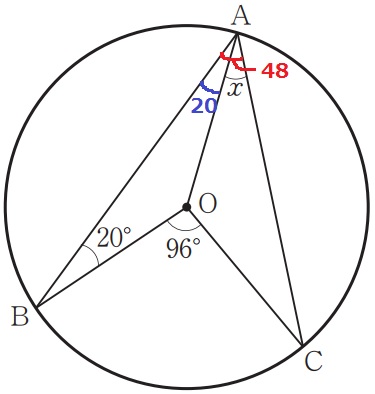
∠ＢＯＣの円周角で、∠ＢＡＣ＝96÷２＝48°
半径より△ＡＢＯは二等辺三角形、∠ＢＡＯ＝20°
ｘ＝48－20＝28°

（７）　53.1％

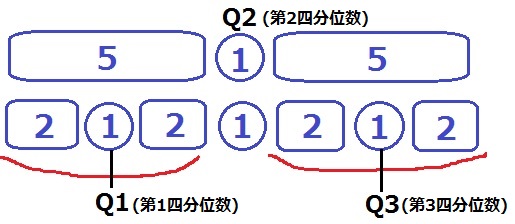
11人のQ2（中央値；第２四分位数）は６番目。
下位５つと上位５つのそれぞれの真ん中を求めると、
下から３番目がＱ1（第１四分位数）で、上から３番目がＱ3（第３四分位数）
四分位範囲＝Ｑ3－Ｑ1＝９－４＝５回
*８回の誤答が多かった。最大値－最小値をしたと思われるが、これは範囲（レンジ）

（８）　62.2％
ア：数直線で考えるとわかりやすいかな？
０＜ａ＜ｂだから、√ａ＜√ｂが成り立つ。〇
イ：平方数で考えてみよう。
√１＋√４＝１＋２＝３、√（１＋４）＝√５、√５≠３。×
ウ：√（－ａ）²＝√ａ。×
エ：２乗してａになる数をａの平方根という。
－√ａもａの平方根。×
ア

大問２（作図・方程式）

（１）　65.2％

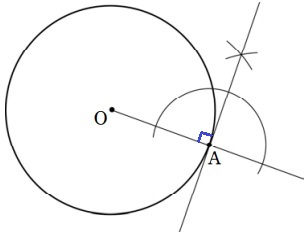
接線の作図。
Ａを通る半直線ＯＡの垂線を描けばいい。

（２）あ…88.8％、い…67.7％、う…64.1％、え…32.7％！、番号…59.1％
誘導に従う。
ａｘ＋４ｂ＝20に（ａ、ｂ）＝（２、３）を代入。
２ｘ＋４×３＝20
ｘ＝４

ａｘ＋４ｂ＝20をｘについて解く。
ａｘ＝20－４ｂ　←両辺を÷ａ
ｘ＝（20－４ｂ）/ａ
ｘの値が負になる場合を考える。
分子に注目して、20－４ｂ＜０のときにｘは負になる。
これはｂ＝６のときだけ。
ｂは小さいサイコロの目だから、「小さいサイコロの出た目が６のとき」にｘは負。

ｂ＝６を代入して、ｘ＝（20－４×６）/ａ＝－４/ａ
ｘが負の整数となるには、ａが４の約数でなければならない。
ａは大きいサイコロの目だから、「大きいサイコロの出た目の数が４の約数になるとき」ｘは負の整数。
あ…４、い…20－４ｂ、う…６、え…４、ア…③

イ　26.1％！
４の約数は【１、２、４】
ｂ＝６で、ａ＝１、２、４の３通り。
確率は３/36＝１/12

大問３（図形）

（１）ア　65.9％

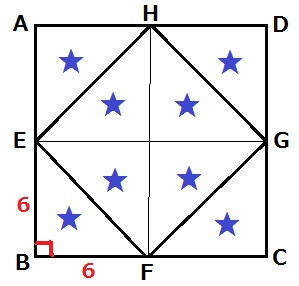
△ＥＦＢは直角二等辺三角形。
辺の比は１：１：√２だから、ＥＦ＝６√２ｃｍ

イ　32.9％！
前図より、面ＥＦＧＨは正方形ＡＢＣＤの面積の半分である。

錘の頂点をＯとする。
四角錘Ｏ―ＥＦＧＨの体積を①とすると、
底面積が２倍である四角錘Ｏ―ＡＢＣＤの体積は②。
錘の体積の３倍が柱だから、立方体の体積は⑥である。

立方体から四角錘Ｏ―ＥＦＧＨを抜き取ると、体積は⑥⇒⑤に減る（水の体積は⑤）
底面積は等しく高さが減るので、水面の高さは12×５/６＝10ｃｍ

（２）ア　あ…51.0％、い…53.7％、う…58.3％
△ＢＦＨ≡△ＤＥＧの証明。
やや変わった雰囲気がする。誘導に従う。

ＡＤ//ＢＣの錯角で、∠ＦＢＨ＝∠ＥＤＧ　…①
菱形の対角は等しいから、∠ＢＣＤ＝∠ＢＡＤ＝ｘ
折り返しで、∠ＤＨＦ＝∠ＢＧＥ＝ｘ
∠ＢＨＦ＝∠ＤＧＥ＝180－ｘ　…②

菱形の対辺は等しく、合同図形の対応する辺より、ＡＢ＝ＣＤ＝ＢＧ＝ＤＨ（〇）
ＢＨ＝ＢＤ－ＤＨ（〇）、ＤＧ＝ＤＢ－ＢＧ（〇）から、ＢＨ＝ＤＧ　…③
①、②、③より、１辺と両端角が等しいので合同となる。
あ…∠ＢＨＦ＝∠ＤＧＥ、い…ＢＨ＝ＤＧ、う…１辺と両端角

イ（ア）　37.8％

折り返しの合同で、∠ＥＧＢ＝108°
菱形の辺は等しいから、△ＡＢＤは二等辺三角形。
∠ＡＤＢ＝（180－108）÷２＝36°
△ＥＤＧで外角定理→∠ＧＥＤ＝108－36＝72°

（イ）　10.8％！
本問も角度の情報を使う。

∠ＥＧＤ＝180－108＝72°
底角が等しいので、△ＤＥＧは二等辺三角形。これに気がつけるかがポイント。
ＥＧ＝ＥＡ＝ｘとする。

菱形の１辺はｘ＋４。
菱形ＡＢＣＤの外周は、４（ｘ＋４）＝４ｘ＋16ｃｍ
四角形ＡＢＧＥの外周は、２（ｘ＋４）＋２ｘ＝４ｘ＋８ｃｍ
両者の差は、（４ｘ＋16）－（４ｘ＋８）＝８ｃｍ

大問４（関数）

（１）　79.8％
ｙ＝16/ｘにｘ＝－４を代入。
ｙ＝16÷（－４）＝－４
*誤答は符号のつけ忘れが多かった。

（２）　50.4％
Ａ（－４、－４）⇒Ｂ（８、２）
右に12、上に６だから、傾きは６/12＝１/２
これと平行なので傾きは１/２。切片ＰはＢのｙ座標と同じ２。
ｙ＝１/２ｘ＋２

（３）ア　55.5％
Ｓのｘ座標はｔである。
ｙ＝１/４ｘ²にｘ＝ｔを代入して、ｙ＝１/４ｔ²
*無解答も多かった。

イ　8.1％!!

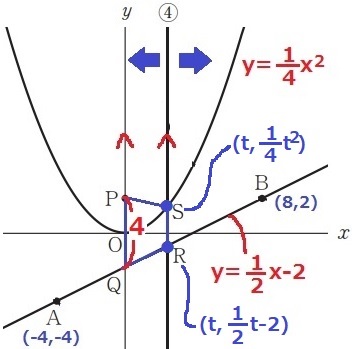
ＡＢの傾きは１/２なので、Ａから右に４、上に２移動して、
ＡＢの切片Ｑは－４＋２＝－２
ＡＢ；ｙ＝１/２ｘ－２
また、Ｐのｙ座標は２だから、ＰＱ＝２－（－２）＝４

ＰＱ//ＳＲなのでＰＱ＝ＳＲ＝４となれば、１組の対辺が平行でかつ長さが等しく、
四角形ＰＱＲＳが平行四辺形になる。

Ｓのｙ座標が１/４ｔ²、Ｒのｙ座標が１/２ｔ－２だから、
ＳＲ＝１/４ｔ²－（１/２ｔ－２）＝４
１/４ｔ²－１/２ｔ－２＝０　←４倍
ｔ²－２ｔ－８
＝（ｔ－４）（ｔ＋２）＝０
ｔ＝－２、４
*無解答が多かった。

大問５（方程式）

（１）あ…59.1％、い…26.5％！
最初の表を読み取れるかどうかで点差が開く。

Ｂは前月までのＡの和。５月のＢは６＋２＝８
Ｃは基準である水曜（７の倍数）を０として、ズレを＋３～－３の範囲で表す。
11は14の３つ手前だから－３。
７からカウントすると＋４で不適。
あ…８、い…－３

（２）　51.3％
５月のＣを見る。
５月１日は基準の水曜に＋１だから木曜日。

（３）　39.1％
７月のＣを見ると、７月１日は－１だから火曜日。
その５日後が最初の日曜なので６日。

（４）ア　24.4％！
カレンダーで真上にある数は７日前。
ａの７日前はａ－７。
*無解答も多かった。

イ　15.2％！

続きのマスを埋める。
問題のカレンダーは１日が月曜なので、基準の水曜の２日前⇒Ｃが－２。
日数は30日だから、30日の月でＣが－２は９月しかない。

ａ²＋（ａ－７）²＝（ａ＋２）²
ａ²＋ａ²－14ａ＋49＝ａ²＋４ａ＋４
ａ²－18ａ＋45
＝（ａ－15）（ａ－３）＝０
ａの真上に数があるということは、ａは少なくとも８日以降でなくてはならない。
（*１日の７日後が８日）
ａ＞８より、ａ＝15
したがって、９月15日。
*無解答も多かった。
公立高校入試解説ページに戻る