2022年度　大阪府公立高校入試Ｃ問題過去問【数学】解説

平均66.1点（前年比；＋9.1点）
問題はコチラ→ＰＤＦファイル
2022年度・大阪（数学）Ａ問題、Ｂ問題の解説はコチラ。

大問１（小問集合）

（１）　95.0％
（３ａ－ｂ）/４－（ａ－２ｂ）/６
＝｛３（３ａ－ｂ）－２（ａ－２ｂ）｝/12
＝（９ａ－３ｂ－２ａ＋４ｂ）/12
＝（７ａ＋ｂ）/12

（２）　89.8％
ｘ－16ｙ＋10＝５ｘ－14＝－８ｙ
ｘ－16ｙ＋10＝－８ｙ
ｘ－８ｙ＝－10　…①
５ｘ－14＝－８ｙ
５ｘ＋８ｙ＝14　…②

①＋②をして、６ｘ＝４
ｘ＝２/３
①に代入、８ｙ＝２/３＋10＝32/３
ｙ＝４/３
ｘ＝２/３、ｙ＝４/３

（３）　97.0％
ｘ²－ｙ²
＝（ｘ＋ｙ）（ｘ－ｙ）
＝｛（√15＋√５）＋（√15－√５）｝｛（√15＋√５）－（√15－√５）｝
＝２√15×２√５
＝20√３

（４）　86.0％
グラフでは右上だからａは正のように思えるが、
ちゃんと式を整理してみよう。
ａｘ＋ｂｙ＝１
ｂｙ＝－ａｘ＋１
ｙ＝－ａ/ｂｘ＋１/ｂ

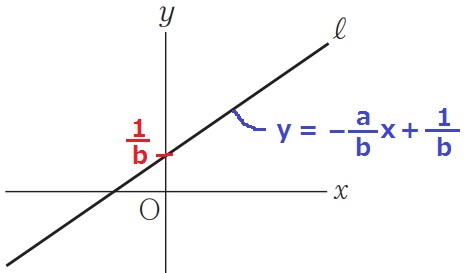
切片１/ｂはｘ＞０だから正。
【１（正）÷ｂ＝正】→ｂは正の数である。
グラフは右上だから、－ａ/ｂは正。
【－ａ/ｂ＝－ａ÷ｂ（正）＝正】→－ａは正→ａは負の数。
ウ

2022年度　埼玉県公立高校入試・学校選択過去問【数学】解説

平均42.6点（前年比；－13.4点）問題はコチラ→ＰＤＦファイル2022年度・埼玉数学（共通問題）の解説はコチラ。大問１（小問集合）（１）　78.5％６ｘｙ2÷（－３/５ｘｙ）÷（－２ｘ）3＝６ｘｙ2÷（－３/５ｘｙ）÷（－８ｘ3）＝５ｙ...

sabotensabo.com

2022.03.01

平均ダダ下がりの埼玉学校選択・大問１（９）で似たようなのが出ています。

（５）　81.0％
３枚の取り出し方は、₃Ｃ₂×₃Ｃ₁＝９通り
ａ＜ｂ＜ｃの条件で、ａｃ/ｂが自然数となる組み合わせを探す。
分母のｂで場合分け。
●ｂ＝１
ｂは２番目に小さい数でなくてはならない。×
●ｂ＝２
ａ＝１だから（１×ｃ）/２
ｃは箱Ａから選ぶので、ｃ＝４、６
●ｂ＝３
３は箱Ｂにあるので、ａは箱Ａの２。
（２×ｃ）/３で、箱Ａから選んでｃ＝６
●ｂ＝４
分母が４＝２²ということは、分子に２の素因数が２つ必要だが、
箱Ａは２と６、箱Ｂは奇数しかないので、分子を４の倍数にできない！×
●ｂ＝６
ｃ＝９が確定。（ａ×９）/６でａ＝２、４
●ｂ＝９
ｂは２番目に小さい数である。×
以上５通り、確率は５/９。

（６）　81.0％
度数分布表が見当たらないが、分数の問題に帰結する。
215ｃｍ以上220ｃｍ未満の階級の度数で、
サッカーをｘとすると、バレーはｘ＋３。
相対度数で等式を立てると、
ｘ/32＝（ｘ＋３）/20　←通分の要領で…
20ｘ＝32（ｘ＋３）
ｘ＝８
８人

（７）　69.0％
ｍの十の位をａ、一の位をｂとする（ａ≠０）
ｍ＝10ａ＋ｂ
ｎ＝ａ＋ｂ

11ｎ－２ｍ
＝11（ａ＋ｂ）－２（10ａ＋ｂ）
＝11ａ＋11ｂ－20ａ－２ｂ
＝－９ａ＋９ｂ
＝９（ｂ－ａ）

50≦９（ｂ－ａ）≦60
９（ｂ－ａ）は９の倍数だから、９×６＝54しかない。
ｂ－ａ＝６
（ｂ、ａ）＝（９、３）（８、２）（７、１）
*ａ≠０だから（６、０）は×！
ｍ＝10ａ＋ｂなので、ｍ＝17、28、39

（８）　62.3％
答案では途中式を含めた求め方も書く。
平行四辺形の頂点で、かつ直線ℓ上にあるＤに目星をつける。
Ｄ座標をｔで表せないか。

Ａ（ｔ、－１/３ｔ²）Ｂ（－ｔ、１/３ｔ²）
平行四辺形ＡＢＤＥでＡからＥまでの移動とＢからＤまでの移動は同じ。
Ｂから左にｔ、下に４移動してＤなので、Ｄのｘ座標は－２ｔ。
これを直線ℓの式に代入して、ｙ＝１/３×（－２ｔ）－１＝－２/３ｔ－１
Ｄ（－２ｔ、－２/３ｔ－１）

ＣＥ＝４ｃｍ、Ｄのｙ座標と立式する。
１/３ｔ²－（－２/３ｔ－１）＝４
ｔ²＋２ｔ－９＝０
解の公式を適用、ｔ＞０よりｔ＝－１＋√10

大問２（平面図形）

（１）　91.0％
半径がａ/２ｃｍの円の面積を求める。
（ａ/２）²π
＝πａ²/４ｃｍ²

（２）　58.9％
△ＡＢＣ∽△ＣＯＧの証明。

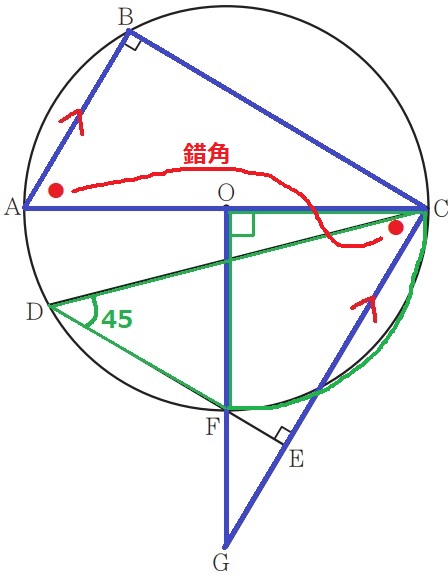
ＡＢ//ＧＣの錯角で、∠ＢＡＣ＝∠ＯＣＧ
もう１つの等角を見抜けるか。
ここで妙な位置にある直角二等辺三角形ＤＥＣを使う。
∠ＣＤＦ＝45°は孤ＦＣに対する円周角で、
この中心角にあたる∠ＣＯＧ＝45×２＝90°
∠ＡＢＣ＝∠ＣＯＧ
２角が等しいから∽。

（３）①　91.0％
ＯＧは△ＣＯＧの１辺⇒前問の相似を試みる。

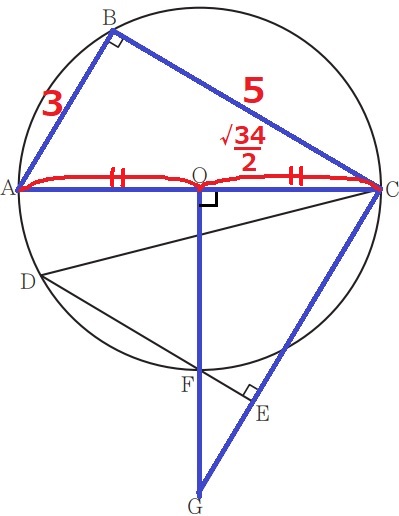
△ＡＢＣで三平方→直径ＡＣ＝√34ｃｍ
半径ＯＣ＝√34/２ｃｍ
△ＡＢＣ∽△ＣＯＧより、ＡＢ：ＢＣ＝ＣＯ：ＯＧ＝３：５
ＯＧ＝√34/２×５/３＝５√34/６ｃｍ

②　20.8％！

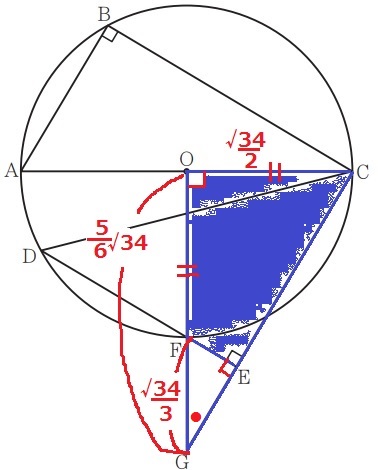
ＯＧとＯＣの長さがわかったので△ＣＯＧの面積がでる。
△ＣＯＧから△ＦＥＧをひけば、求積すべき四角形ＯＦＥＣがでる。
２角相等で△ＣＯＧ∽△ＦＥＧ
半径でＯＦ＝ＯＣ＝√34/２ｃｍ
ＦＧ＝５√34/６－√34/２＝√34/３ｃｍ

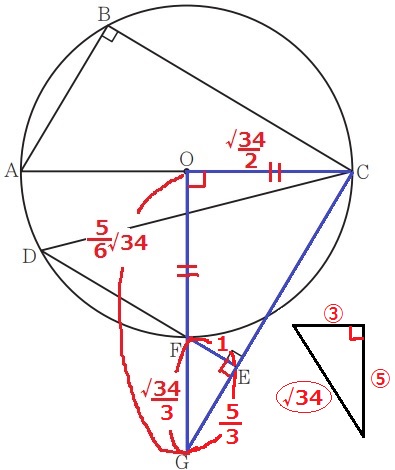
相似比は△ＡＢＣと同じ、３：５：√34。
ＦＥ＝√34/３×③/〇√34＝１ｃｍ
ＥＧ＝１×⑤/③＝５/３ｃｍ
四角形ＯＦＥＣの面積は、√34/２×５√34/６÷２－５/３×１÷２
＝25/４ｃｍ²

＠別解＠
ＯＧの誘導無しで解いてみます。

△ＡＢＣ∽△ＣＯＧの●＋×＝90°から、∠ＢＣＥ＝90°
ＢＡとＥＤを延長、交点をＨとする。
四角形ＢＨＥＣは長方形である。
ＡＤを結ぶ。

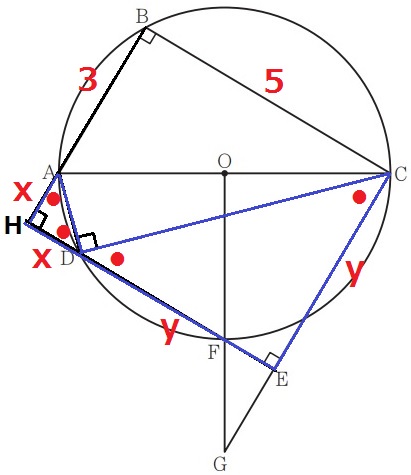
半円の弧に対する円周角で、∠ＡＤＣ＝90°
△ＣＤＥは直角二等辺三角形。●＝45°だから△ＡＤＨも直角二等辺。
ここで、ＡＨ＝ＨＤ＝ｘ、ＣＥ＝ＥＤ＝ｙとする。
長方形の縦の長さで、３＋ｘ＝ｙ　…①
横の長さで、ｘ＋ｙ＝５　…②
①、②の連立を解くと、ｘ＝１、ｙ＝４

直角二等辺ＡＤＨで１：１：√２⇒ＡＤ＝√２ｃｍ
つぎに、△ＡＣＤと△ＦＣＥに着目する。
∠ＡＤＣ＝∠ＦＥＣ＝90°
直角二等辺ＣＯＦの内角で∠ＯＣＦ＝45°
直角二等辺ＣＤＥの内角で∠ＤＣＥ＝45°
これらからあいだの角の∠ＤＣＦをひいて、∠ＡＣＤ＝∠ＦＣＥ
２角相等で△ＡＣＤ∽△ＦＣＥ
相似比はＤＣ：ＥＣ、すなわち、直角二等辺ＣＤＥの辺の比√２：１。
ＡＤ：ＦＥ＝√２：１
ＦＥ＝１ｃｍ

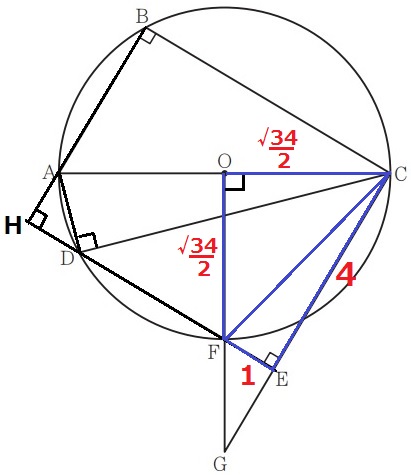
四角形ＯＦＥＣ＝△ＣＯＦ＋△ＦＣＥ
＝√34/２×√34/２÷２＋４×１÷２
＝17/４＋２
＝25/４ｃｍ²

大問３（空間図形）

（１）①　91.0％

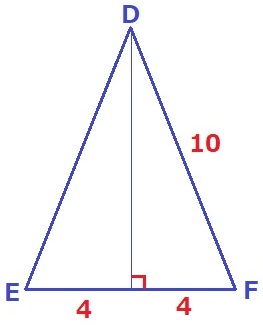
△ＤＥＦは二等辺三角形。
高さを三平方で算出→２√21ｃｍ
面積は、８×２√21÷２＝８√21ｃｍ²

②　65.0％

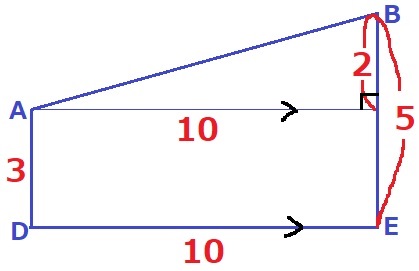
Ａを通るＤＥに平行な線分をひく。
三平方を適用して、ＡＢ＝２√26ｃｍ

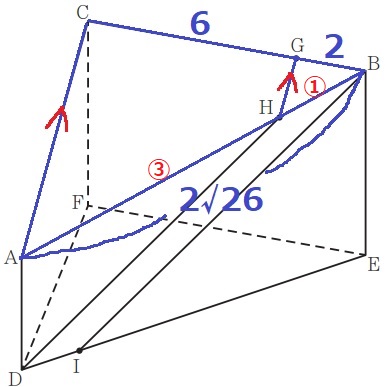
ＡＣ//ＨＧより、△ＡＢＣ∽△ＨＢＧ
ＡＨ：ＨＢ＝ＣＧ：ＧＢ＝③：①
ＨＢ＝２√26×①/④＝√26/２ｃｍ

③　12.0％！

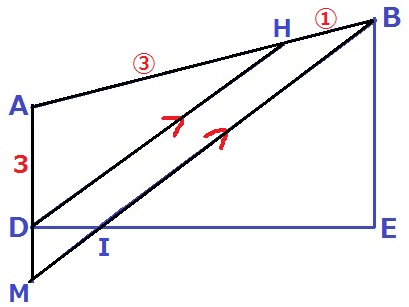
ＡＤとＢＩを延長、交点をＭとする。
ＤＨ//ＭＢから△ＡＤＨ∽△ＡＭＢより、ＡＤ：ＤＭ＝③：①
ＤＭ＝１ｃｍ

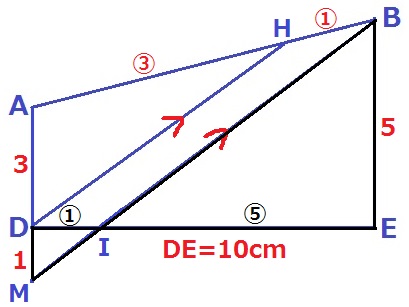
△ＤＩＭ∽△ＥＩＢより、ＤＩ：ＩＥ＝①：⑤
ＤＥ＝10ｃｍなので、ＤＩ＝10×①/⑥＝５/３ｃｍ

（２）①　74.0％

ＡＤ//ＫＪ//ＢＥから平行線と線分の比よりＡＫ：ＫＢ＝４：６＝②：③
ＬＫ//ＣＢで△ＡＫＬ∽△ＡＢＣ、ＬＫ＝８×②/⑤＝16/５ｃｍ

②　8.0％!!

断頭三角柱。
上図のように、各辺の中点にＮ・Ｏ・Ｐ・Ｑをつくる。
（立体を上からみるとＡＮは二等辺ＡＢＣを真っ二つに割る線分である）
対称面である△ＰＮＯを底面とみなす。
前問のＤＪ：ＪＥ＝２：３から、ＤＱ：ＱＯ＝②：③
（１）①の２√21ｃｍをもってきて、ＱＯ＝２√21×③/⑤＝６√21/５ｃｍ
△ＰＮＯの底辺はＮＯ＝５ｃｍ、高さは６√21/５ｃｍ。

立体の高さはＢＣ・ＥＦ・ＫＬの平均で、（８＋８＋16/５）÷３＝32/５ｃｍ
立体の体積は、５×６√21/５÷２×32/５＝96√21/５ｃｍ³
公立高校入試解説ページに戻る