2023年度　都立国立高校過去問【数学】大問３解説

ＰＤＦファイル
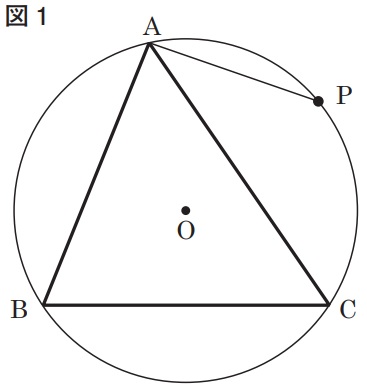
　下の図１で、点Ｏは、∠ＡＢＣ＜90°、∠ＡＣＢ＜90°である△ＡＢＣの３つの頂点を通る円の中心である。円Ｏの周上にあり、頂点Ａ、頂点Ｂ、頂点Ｃのいずれにも一致しない点をＰとし、頂点Ａと点Ｐを結ぶ。次の各問に答えよ。

〔問１〕
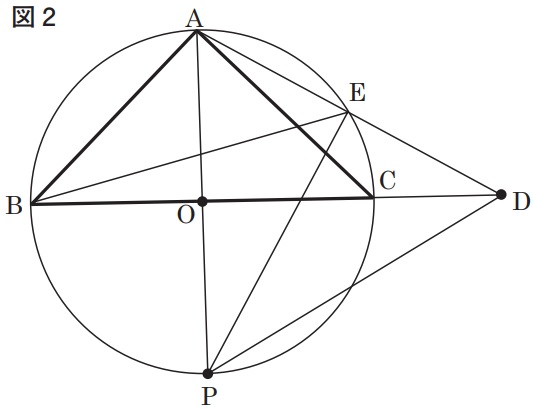
下の図２は、図１において、辺ＢＣと線分ＡＰがともに点Ｏを通るとき、辺ＢＣをＣの方向に延ばした直線上にある点をＤとし、頂点Ａと点Ｄを結び、線分ＡＤと円Ｏとの交点をＥとし、点Ｂと点Ｅ、点Ｅと点Ｐ、点Ｐと点Ｄをそれぞれ結び、ＡＥ＝ＤＥの場合を表している。∠ＥＰＤ＝30°のとき、∠ＤＢＥの大きさは何度か。

〔問２〕
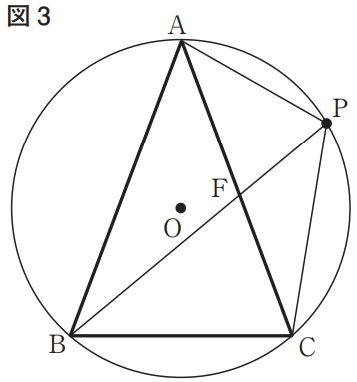
下の図３は、図１において、点Ｐが頂点Ｂを含まない弧ＡＣ上にあり、ＡＢ＝ＡＣのとき、頂点Ｂと点Ｐ、頂点Ｃと点Ｐをそれぞれ結び、辺ＡＣと線分ＢＰとの交点をＦとした場合を表している。ＣＰ＝ＣＢとなるとき、△ＡＦＰは二等辺三角形であることを証明せよ。

〔問３〕
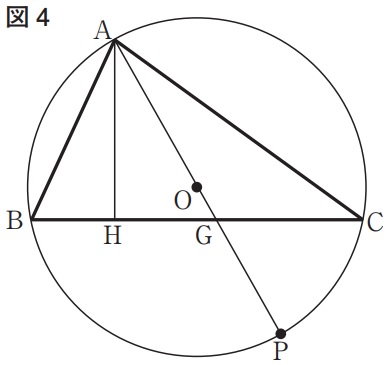
下の図４は、図１において、線分ＡＰが点Ｏを通るとき、頂点Ａから辺ＢＣに垂線を引き、辺ＢＣとの交点をＨ、線分ＡＰと辺ＢＣとの交点をＧとした場合を表している。ＡＰ＝20ｃｍ、ＡＢ＝12ｃｍ、ＢＨ＝ＧＨのとき、ＣＧ：ＣＡを最も簡単な整数の比で表せ。また、辺ＡＣの長さは何ｃｍか。

〔問１〕

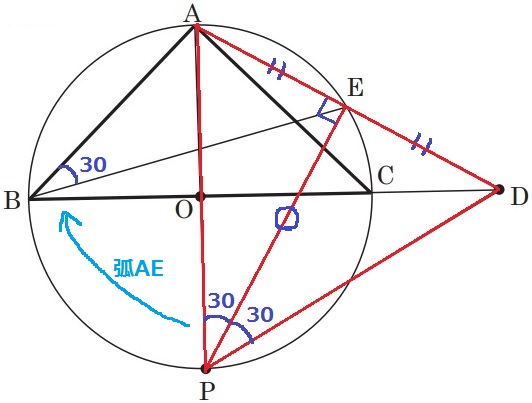
直径ＡＰに対する円周角→∠ＡＥＰ＝∠ＤＥＰ＝90°
ＡＥ＝ＤＥ、共通辺ＰＥより、２辺と間の角が等しいので△ＡＰＥ≡△ＤＰＥ
対応する角で、∠ＡＰＥ＝30°

弧ＡＥの円周角から、∠ＡＢＥ＝30°
ここで△ＡＰＤに着目すると、
内角が30°ー60°ー90°の三角形を２つ組み合わせた三角形なので正三角形。

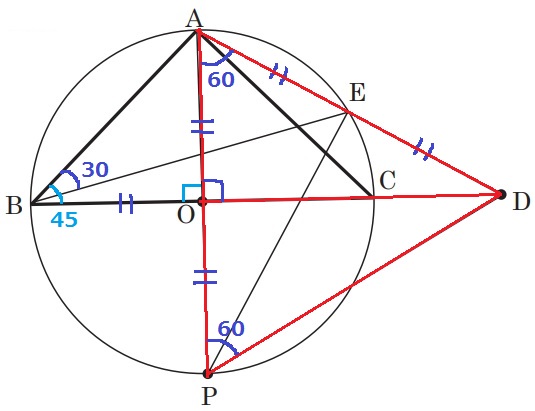
半径ＡＯ＝ＰＯより、正三角形の半分である△ＡＯＤの内角は30°ー60°ー90°
∠ＡＯＢ＝90°→△ＡＢＯは直角二等辺で∠ＡＢＯ＝45°
∠ＤＢＥ＝45－30＝15°

〔問２〕
△ＡＦＰが二等辺である証明。

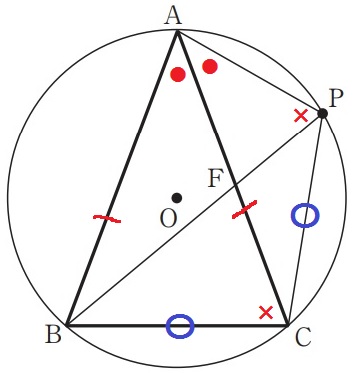
△ＢＣＦを経由しても解けるが、直接、相似を指摘することができる。
弧ＡＢの円周角より、∠ＡＣＢ＝∠ＡＰＦ（×）
ＣＢ＝ＣＰ→弧ＣＢ＝弧ＣＰ→∠ＢＡＣ＝∠ＦＡＰ
２角相等だから、△ＡＢＣ∽△ＡＦＰ
△ＡＢＣはＡＢ＝ＡＣの二等辺なので、△ＡＦＰも二等辺である。

〔問３〕

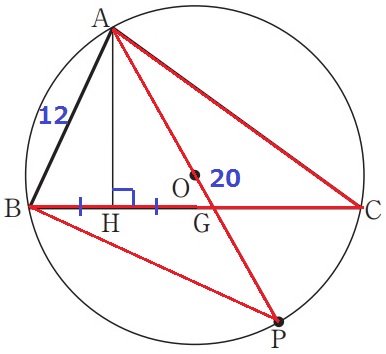
ＣＧ：ＣＡに対応する辺の比を探す。
ＢＰに補助線を引くと、対頂角や円周角で２角相等→△ＡＣＧ∽△ＢＰＧ
ＣＧ：ＣＡ＝ＰＧ：ＰＢを求めればいい。

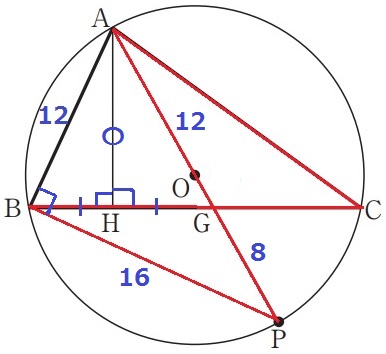
ＢＨ＝ＧＨ、∠ＡＨＢ＝∠ＡＨＧ、共通辺ＡＨ→２角と間の角度が等しく、△ＡＢＨ≡△ＡＧＨ
ＡＢ＝ＡＧ＝12ｃｍ
ＰＧ＝20－12＝８ｃｍ

また、直径ＡＰに対する円周角で∠ＡＢＰ＝90°
△ＡＢＰの辺の比は３：４：５→ＰＢ＝16ｃｍ
ＣＧ：ＣＡ＝ＰＧ：ＰＢ＝８：16＝１：２

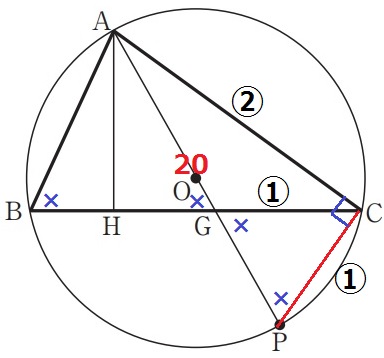
１：２を活用したい。ＰＣに補助線を入れると三平方が使えそう。
対頂角と弧ＡＣの円周角（×）より、二角相等で△ＡＢＧ∽△ＣＰＧ
△ＡＢＧは等辺12ｃｍの二等辺→△ＣＰＧも二等辺。
（ＧＣ＝①、ＡＣ＝②とするとＰＣ＝①）

直径ＡＰに対する円周角で∠ＡＣＰ＝90°
ＰＣ＝ｘ、ＡＣ＝２ｘとおいて、△ＡＰＣで三平方。
ｘ²＋（２ｘ）²＝20²
ｘ²＝80
ｘ＞０より、ｘ＝４√５ｃｍ
ＡＣ＝２ｘ＝８√５ｃｍ
ＣＧ：ＣＡ＝１：２、ＡＣ＝８√５ｃｍ
国私立高校入試解説ページに戻る