2021年度　岡山朝日高校過去問【数学】大問５解説

問題ＰＤＦ
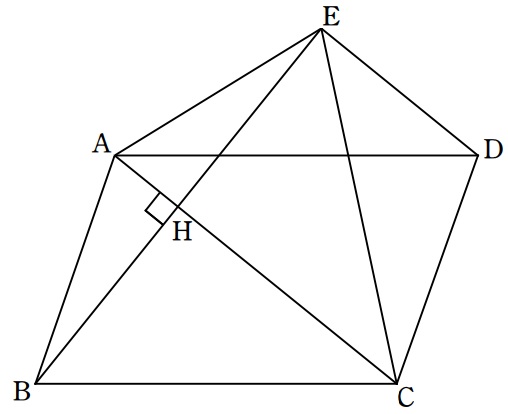
下の図のように、周の長さが20である平行四辺形ＡＢＣＤがあり、ＡＣ＝ＢＣ＝６である。
Ｂから直線ＡＣにひいた垂線と直線ＡＣとの交点をＨとし、直線ＢＨ上にＢとは異なる点Ｅを、
ＡＢ＝ＡＥを満たすようにとる。

①
ＡＢの長さを求めなさい

②
△ＡＢＣ≡△ＡＥＣであることを証明しなさい。

③
ＡＨとＤＥの長さをそれぞれ求めなさい。

④
３点Ａ、Ｅ、Ｄを通る半径を求めなさい。

②　正答率45.6％（部分点50.9％）
△ＡＢＣ≡△ＡＥＣの証明。

ＡＢ＝ＡＥ＝４　…①
共通辺ＡＣ　…②
２辺のあいだの角である∠ＢＡＣ＝∠ＥＡＣを指摘したいが、
二等辺三角形や平行四辺形を手がかりにしても角の情報がなかなかでてこない(´～`)

そこで∠ＡＨＢ＝90°に着目する。
△ＡＢＨと△ＡＥＨにおいて、∠ＡＨＢ＝∠ＡＨＥ＝90°
共通辺ＡＨ、ＡＢ＝ＡＥより、斜辺と他の１辺が等しい直角三角形。
△ＡＢＨ≡△ＡＥＨ

対応する角が等しく、∠ＢＡＣ＝∠ＥＡＣ…③
①、②、③より、２辺とあいだの角度が等しく、△ＡＢＣ≡△ＡＥＣ

③　正答率50.7％、14.2％！

↑これが見えたら、しめたもの。
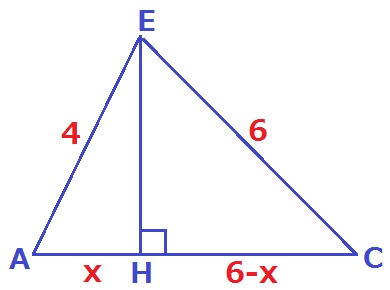
ＡＨ＝ｘとおくと、ＨＣ＝６－ｘ

左右の直角三角形で三平方の方程式。
４²－ｘ²＝６²－（６－ｘ）²
16－ｘ²＝36－36＋12ｘ－ｘ²
ｘ＝４/３
ＡＨ＝４/３

このあとからキツくなってくる:;(∩´＿`∩);:

二等辺三角形と合同から等角に印をつける。
さらに、ＡＢ//ＤＣより、錯角で∠ＡＣＤ＝●
平行四辺形の対角より、∠ＡＤＣ＝●

ここでＡ・Ｃ・Ｄ・Ｅに注目する。
直線ＡＣについて同じ側にある２点Ｄ、Ｅについて、
∠ＡＤＣ＝∠ＡＥＣが成り立ち、４点Ａ・Ｃ・Ｄ・Ｅは同一円周上にある。（円周角定理の逆）

ＡＥ＝ＣＤ→弧ＡＥ＝弧ＣＤ
円周角定理より、∠ＡＤＥ＝∠ＣＡＤ（×）
錯角が等しいので、ＡＣ//ＥＤとなる。
∠ＥＡＣ＝∠ＤＣＡとあわせると、四角形ＡＣＤＥは等脚台形である。

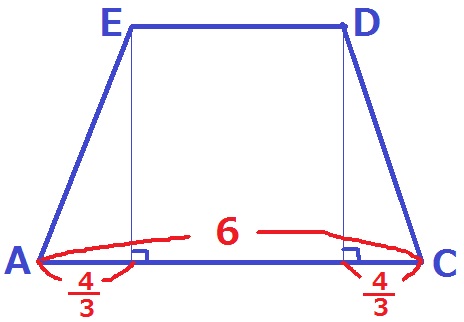
等脚台形は左右対称。
ＤＥ＝６－４/３×２
＝10/３

④　正答率2.4％!!
この手の問題は、直径に対する円周角が直角であることから、
①直角を探す⇒②直径の中点が円の中心、という流れが典型的だが、
本問では直径とおぼしき線分が見当たらない(´°ω°`;)

３点Ａ・Ｅ・Ｄを通る円⇒等脚台形ＡＣＤＥが接する円⇒△ＡＣＥが接する円
作図問題にでてくるとおり、外接円の中心は各辺の垂直二等分線の交点である。
ＡＣの中点をＰ、ＡＥの中点をＱとし、これらを通る２本の垂線の交点が中心Ｏとなる。

また、△ＡＣＥは二等辺三角形だから、底辺の垂直二等分線ＱＯはＣを通る。
△ＡＣＱで三平方→ＣＱ＝４√２

２角相等で△ＣＡＱ∽△ＣＯＰ
ＯＣ＝６×３/４√２＝９√２/４
国私立高校入試解説ページに戻る