問題PDF
(1)
4けたの整数について、次の性質(P)を考えます。
性質(P)千の位の数を十の位の数、百の位の数を一の位とする2けたの整数で割り切れる。
例えば、
1900=19×100、1352=13×104
ですから、1900や1352は性質(P)を満たします。
性質(P)を満たす4けたの整数の中で2023以下のものは全部で何個ありますか。
(2)
4けたの整数について、次の性質(Q)を考えます。
性質(Q)百の位の数を十の位の数、十の位の数を一の位の数とする2けた以下の整数で割り切れる。
例えば、
6786=78×87、6076=7×868
ですから、6786や6076は性質(Q)を満たします。
これらの例のように、千の位と一の位がともに6であり、性質(Q)を満たすような4けたの整数は全部で何個ありますか。
(3)
4けたの整数について、次の性質(R)を考えます。
性質(R)十の位の数を十の位の数、一の位の数を一の位の数とする2けた以下の整数で割り切れる。
最初に2けたの整数を1つ選んで、その整数の十の位の数を千の位の数に、一の位の数を百の位の数とする4けたの整数をつくります。そして、その中で性質(R)を満たすものが何個あるかを考えます。例えば、最初に20を選んだときは、
2025=25×81、2008=8×251
ですから、2025や2008は性質(R)を満たします。
(ⅰ)上の例のように最初に選んだ2けたの整数が20のときは、性質(R)を満たす4けたの整数を全部で何個つくることができますか。
(ⅱ)すべての2けたの整数に対して、性質(R)を満たす4けたの整数がそれぞれ全部で何個つくられるかを考えたとき、その個数は最も少なくて何個ですか。また、そのときに最初に選んだ2けたの整数を求めなさい。
(ⅲ)すべての2けたの整数に対して、性質(R)を満たす4けたの整数がそれぞれ全部で何個つくられるかを考えたとき、その個数が(ⅱ)の答えより1個だけ多いような2けたの整数として考えられるものを小さい順に5個求めなさい。
@解説@
(1)
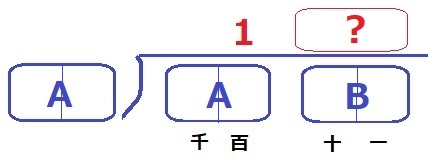
ある4桁の整数で千と百の位の2桁をA、十と一の位の2桁をBとして、
筆算を書いて割り切れた様子が上図である。
A÷A=1、B÷Aが割り切れる→BはAの倍数である。
●A=【10】
Bは00、10、20、30…90の10個。
*Bは00を含む!
●A=【11】
Bは00、11、22…99の10個。
●A=【12】
Bは00、12、24…96の9個。
●A=【13】
Bは00、13、26…91の8個
●A=【14】
Bは00、14…98の8個。
●A=【15】
Bは00、15…90の7個。
●A=【16】
Bは00、16…96の7個。
●A=【17】
Bは00、17…85の6個
●A=【18】
Bは00…90の6個
●A=【19】
Bは00…95の6個
●A=【20】
2023以下なので、Bは00と20の2個しかない。
計79個
(2)
百の位をA、十の位をBとすると、4桁の整数は〔6AB6〕
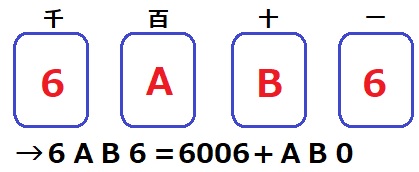
これがABで割り切れる。
ポイントは6AB6=6006+AB0に分けること!
6006+AB0はABの倍数。
→AB0は言わずもがなABで割り切れる。6006がABの倍数であればいい。
ABは2桁以下の6006の約数だが、これがわかっても手間がかかる(;´・ω・)
【6006=6×1001=2×3×7×11×13】
(*1001=7×11×13の素因数分解は有名なのでおさえておく)
素因数の個数で場合分けして99以下になるものを探す。
ABは「2桁以下の整数」だから、1桁(A=0)でもOK。
●素因数1個→2~13の5個。1を忘れずに!AB=01もいける。+1個!
●素因数2個→2×(3~13)の4個、3×(7~13)の3個、7×(11、13)の2個。
●素因数3個→(2、3、7~13)の3個。
●素因数4個→(2、3、7、11)がダメだから無い。
計18個
(3)ⅰ
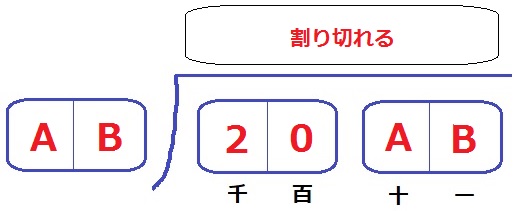
問題文の条件を整理します。
4桁の整数で十の位をA、一の位をBとする。
今、「最初に選んだ2桁」を20にしたので、千の位を2、百の位を0としたら、
20AB÷ABが割り切れた。このようなABはいくつあるかを求める。
ここも、20AB=2000+ABに分解する。
下2桁のABはABの倍数なので、2000はABの倍数である。
→2桁以下の2000の約数を求めればいい。
素因数分解すると、2000=1×2×2×2×2×5×5×5
5の素因数の個数で場合分け。
●5の素因数が0個→1、2、4、8、16
●5の素因数が1個→5、10、20、40、80
●5の素因数が2個→25、50
計12個
ⅱ
本問は千の位と百の位となる「最初に選ぶ2桁の整数」のなかで、ABの個数が最も少なくなる数を探し出す。
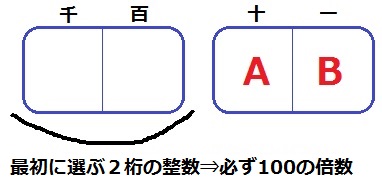
前問の手順をおさらいすると、
〔20AB〕=2000+AB→ABは2桁以下の2000の約数。
4桁の整数を分解し、下2桁のABを00に置き換えてからABの個数を考えた。
そして、置き換えた数は必ず100の倍数である。
(2桁に12を選んだら1200=12×100、37を選んだら3700=37×100)
ABには常に2桁以下の100の約数がはいってくる!
具体的に書くと、〔1・2・4・5・10・20・25・50〕の8個である。
では、AB=8個を維持する理想の2桁はあるのだろうか?
100の約数は絶対くるので、そこに狙いをつけてみる。
100の約数のうち、2桁は〔10・20・25・50〕の4個。
この中で最も約数が少ないのは25である。
25を選んだ場合、2500=25×100
25の約数は〔1・5・25〕
100の約数(2桁)〔1・2・4・5・10・20・25・50〕において、
100以上にならないようにいずれかを5倍したり25倍したらどれかの数字とかぶる!
たとえば、2×5=10…4×5=20…5×5=25…10×5=50…2×25=50…
すべて重複するゆえ、8個をキープする!!
10×100=1000…〔1・2・4・5・8・10・20・25・40・50〕
20×100=2000…〔1・2・4・5・8・10・16・20・25・40・50・80〕前問の12個
50×500=5000…〔1・2・4・5・8・10・20・25・40・50〕
10、20、50は偶数で約数2が邪魔してしまう。
10×100では(10の約数2)×(100の約数4)=8(10の約数2)×(100の約数20)=40が追加。
(1000の倍数は8・40の追加が確定することになる)
20×100では、さらに20の約数4の存在から4×4=16、20×4=80が追加されてしまう。
したがって、最も少ない個数は『8個』で最初に選ぶ2桁の整数は『25』となる。
ⅲ
■再掲■
100の約数(2桁)〔1・2・4・5・10・20・25・50〕
↑絶対に出てきてしまう8個。これに1個だけを足したい。
100の約数は2を含むので、49以下の数字は×!
実際に見てみましょう。
49×100=4900…〔1・2・4・5・7・10・14・20・25・28・35・49・50・70・98〕
↑(49の約数49)×(100の約数2)=98が登場する。約数7もいろいろ邪魔している。
47×100=4700…〔1・2・4・5・10・20・25・47・50・94〕
↑素数であっても(47の約数47)×(100の約数2)=94が登場して10個になってしまう。
ということは、2倍したら3桁(100以上)となり、かつ1以外の約数が1個の数、
すなわち、50以上の素数を拾い上げれば良い。
53×100=5300…〔1・2・4・5・10・20・25・50・53〕
53だけが追加されて9個!
小さい順に並べると、53、59、61、67、71。



コメント