民主主義の基本は多数決だ。
選挙で多数を得た者が当選し、議院内閣制では、選挙で多数を握った政党が内閣を組織。
与党と一体で法案を成立させる。それが、「常識」と思っていた。
だが、昨秋、本屋で一冊の本が目に付いた。書名は『多数決を疑う』。その筆者を訪れた。
―なぜ、多数決を疑っているのですか。
「大きな問題があるからです。特に1位しか当選しない衆議院の小選挙区制度。
有権者は自分の考えの一部に過ぎない『どの候補者を一番支持するか』しか表明できません。
その結果、票の割れが頻発して死票が大量に生まれているのです。
比例区で復活の余地がありますが一部に過ぎません。
民主主義の根本理念は、治める者(政治家)と治められる者(国民)の同一性ですが、
ものすごくズレています。
現在の選挙制度は、少数派はもちろん、(A)多数派すら大事にしていません。」
―多数派もですか。
「多数派は51%を押さえれば勝てる制度です。ところが過去3回の衆議院議員選挙で政権を担った与党は、(B)半分以下の得票率で小選挙区の70%超の議席を獲得しました。多数派の支持を得たとは言えません。
それなのに多数決は疑われないまま使われてきた『文化的奇習』なのです。
(中略) 政策課題が『財政』『外交』『環境』とあるとします。
政策別ではB党支持が多くても、選挙になるとA党が勝つことがあるのです。(表1)
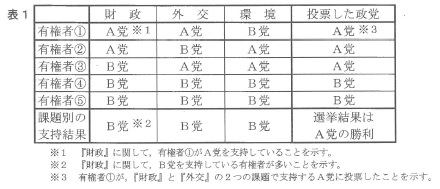
これを(C)オストロゴルスキーのパラドックスと言います。
選挙は、各政策への多数意思を反映するものではないのです。」
(朝日新聞2016年1月9日より)
*オストロゴルスキー・・ロシアの政治学者。アメリカとイギリスの政党制の比較研究で有名。
◆(ア)
下線部(A)『多数派すら大事にしていません』とあるが、
『多数決を疑う』の筆者が言う「多数派」とはどのような人々と考えられるか。
最も適切なものを選びなさい。
1:与党に投票した有権者 2:与党以外の政党に投票した有権者
3:投票に行かなかった有権者 4:選挙権を持たない18歳未満の人々
2
*一般的に考えて、『多数派』とは与党に投票した有権者と考えられるが、
筆者は必ずしも選挙結果が多数派の意思を反映していないと説得する。
これは、”選挙結果には表れていない多数派”が存在するということ。
与党になれなかった野党へ票を投じた有権者を『多数派』と表現し、
現在の選挙制度は彼らを大事にしていないという。
◆(イ)
下線部(B)に関連して、ある選挙において、5つの小選挙区すべてで、
A党とB党の候補者が1人ずつ立候補したとする。
このとき、次の条件のもとで、A党が最も少ない得票数で4つの選挙区で議席を獲得するためには、
5000票のうち何票必要か答えなさい。
また、そのときのA党の得票率は何パーセントになるかを求めなさい。
得票率は、答えの小数第2位を四捨五入して、小数第1位まで答えること。
―条件―
・どの小選挙区の総得票数もそれぞれ1000票ずつで、
すべての票がA党の候補者またはB党の候補者に投票されたものとする。
・どの小選挙区でもA党とB党の得票数は同数にならなかったものとする。
得票数―2004票 得票率―40.1%
*条件を的確に理解できれば、そう難しくはない。
選挙区を①~⑤にわけ、①~④までは過半数の501票をA党がゲット。
残る⑤は1000票すべてがB党にいったとする。
A党の総得票数は、501×4=2004票
得票率は、2004/5000=400.8/1000=40.08/100=40.08% ⇒ 40.1%
A党は得票数4割ほどで、5つの選挙区のうち4つを制覇したことになる。
◆(ウ)
下線部Cに関連する次の文章を読んで、下の条件を満たすように、
表2の空欄にあてはまる人名として、「X」または「Y」を入れなさい。
ただし、解答は、生徒④の太枠の部分のみを解答欄に書きなさい。
オストロゴルスキーのパラドックスについて、中学校の生徒会選挙を例にとって考えてみよう。
ある中学校の生徒会長にXさんが立候補することになった。
Xさんは何事にも積極t系に取り組む活発な生徒で、自分が当選したら、
すべての生徒が『勉強』も『行事』も『部活動』ももっと頑張れるような活気のある学校にしたいと考えている。
一方で、Yさんは全く逆のことを考えている生徒で、何事に対しても消極的であり、
Xさんの考えに反対するために生徒会長に立候補することにした。
―条件―
・投票する生徒(有権者)は5人(生徒①~⑤)とする。
・生徒①と生徒⑤は、『勉強』『行事』『部活動』のすべての課題について、
もっと積極的に取り組むべきだと考えていた。
・生徒②は、『行事』について、もっと積極的に取り組むべきだと考えていた。
・生徒③は、『部活動』について、もっと積極的に取り組むべきだと考えていた。
・それぞれの課題別に見ると、もっと積極的に取り組むべきだという意見が
その課題についても多数であった。
・投票の結果、すべての課題に消極的なYさんが当選した。
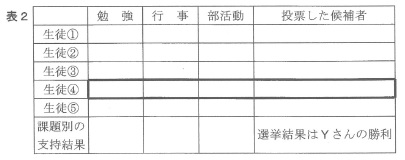
勉強X 行事Y 部活動Y 投票した候補者Y
*論理問題によくある形式。
条件どおりにうめる。
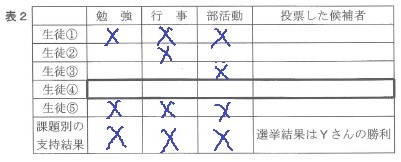
課題別ではすべてXなので、縦の列はXが過半数にする。
ここから、最終的にYが勝つように仕向ける。
右列の『投票した候補者』で②・③・④がYにならなければならない。
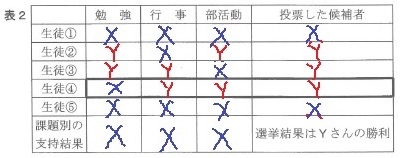
↑最終的にこうなる。
すべての課題でXがYより支持されているのに、天邪鬼のYが当選した。
◆(エ)
比例代表制は、選挙区ごとに各政党の得票数をもとに議席数を配分するもので、
小選挙区制と比べ、有権者の意思をより正確に各党の議席数に反映させることができると言われている。
その議席配分の方法としては、ニューマイヤー方式(ヘア=ニーマイヤー方式)とドント方式が有名で、
今の日本の国政選挙では、ドント方式が採用されている。
まず、ニューマイヤー方式について見てみよう。
たとえば、定数3の比例区でA党が総得票数の3分の2、B党が3分の1を得票し、
C党には票がまったく入らなかったとする。得票数に比例して、A党が2議席、B党が1議席を得て、
C党は議席を得られない、つまり、「定数×各政党の得票率」をその政党の獲得議席数と考えるのである。
しかし、実際の選挙の議席数の計算では割り切れずに端数が出ることが多い。
たとえば定数3、総得票数1500票で、A党700票、B党500票、C党300票だったとする。
この場合、A党の得票率は700/1500なので、獲得議席は3×700/1500=21/15となり、
1議席と端数の6/15議席になる。B党の得票率は500/1500なので、獲得議席はちょうど1議席になる。C党の得票率は300/1500なので、0議席と端数の9/15議席になる。
端数については、議席として配分できておらず、1議席が未配分である。そこで、端数が一番大きいC党がその議席を得ることになり、A党1議席、B党1議席、C党1議席となる。
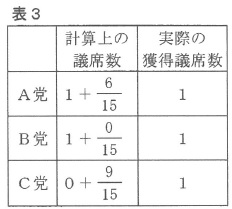
これがニューマイヤー方式の考え方である。
(端数は計算しやすいように分数で示してある。また完全には約分していないところがある)
しかし、C党の300票に対して、A党は700票であり、C党の2倍以上の得票があるのに、議席数は同じ1議席である。仮にA党に2議席を与えたとしても、A党は1議席あたり350票で獲得したことになり、C党の300票を上回っている。
そこで、A党に2議席、B党に1議席、C党は0議席とするほうがよいという考え方もできる。
ドント方式はこのような考え方に基づいており、定数3の議席を配分する場合には、次の表4のように、
各党の得票数を1から順に整数で割って出た数の、大きい順(700、500、300)に順位を決め、
A党、B党、A党の順で議席を割り当てていく。

上で見たように、
(D)ニューマイヤー方式とドント方式では、定数3のときに各党の議席配分に違いが出た。
では、各党の得票数(A党700票、B党500票、C党300票)は変えず、
定数を増やしていった場合、議席配分はどのように変わるのだろうか。
定数4から6までは、両方式による各党の獲得議席配分は同じになる(表5・6)。
(a)
表3・4を参照し、定数が7から9までのときのニューマイヤー方式とドント方式による
各党の獲得議席数をそれぞれ答えなさい。
解答は、解答欄の太枠の部分に書き入れなさい。
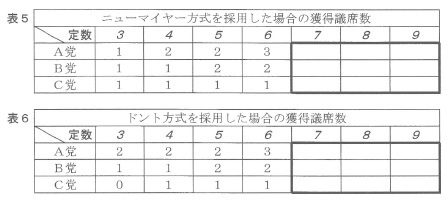
*解答↓
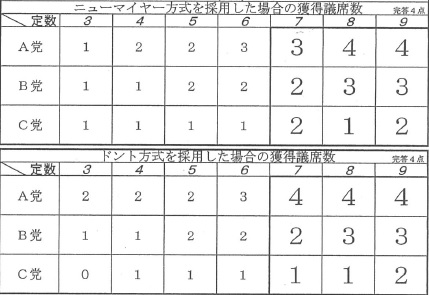
ドント方式の方が馴染みがあるので、先にドント方式から。
| ÷1 | ÷2 | ÷3 | ÷4 | ÷5 | |
| A | 700 | 350 | 233.3 | 175 | 140 |
| B | 500 | 250 | 166.6 | 125 | 120 |
| C | 300 | 150 | 100 | 100 | 60 |
÷1、÷2、÷3・・と除して、上位の者を数える。
上の表では、赤い数字がベスト9。
ニューマイヤー方式は、サボを含め多数の受験生も知らないはずなので、
リード文から現場で計算方法を速攻で学ぶしかないが、そんなに複雑ではない。
@ニューマーヤー方式のルール@
①定数×各政党の得票率
②端数がでた場合は、端数の大きい順に議席を振り分ける。
〔A党700票:B党500票:C票300、計1500票〕
定数7
A;7×700/1500=49/15=3・4/15
B;7×500/1500=35/15=2・5/15
C;7×300/1500=21/15=1・6/15
整数部分の和は6。残り1は端数が最も大きいCに割り当てられる。
A⇒3 B⇒2 C⇒2
定数8
A;8×700/1500=56/15=3・11/15
B;8×500/1500=40/15=2・10/15
C;8×300/1500=24/15=1・9/15
整数部分の和は6。残り2はAとBに割り当てる。
A⇒4 B⇒3 C⇒1
定数9
A;9×700/1500=63/15=4・3/15
B;9×500/1500=45/15=3
C;9×300/1500=27/15=1・12/15
整数部分の和は8。残り1はCに割り当てる。
A⇒4 B⇒3 C⇒2
処理手順が多いので、時間配分に注意!
(b)
現在、ドント方式は日本を含む20ヵ国以上で採用されているのに対し、
ニューマイヤー方式の採用はドイツなどの少数の国にとどまっている。
表5には、このことに関連するニューマイヤー方式による議席配分の問題点が具体的に表れている。この問題点について述べた次の文中の空欄にあてはまる言葉を、「獲得議席」という語を使って、15字以内で書きなさい。
ニューマイヤー方式による議席配分では、定数が〔 〕政党が出ることがある。
増えたのに、獲得議席数が減る
*ニューマイヤー方式の問題点を問う。
前問で答えたニューマイヤー方式の答案を観察しよう。
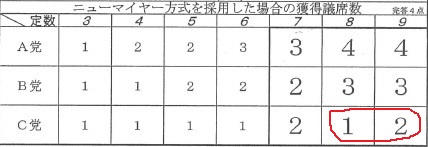
定数が7⇒8に増えたとき、C党の獲得議席数が2議席から1議席に減っている。
普通、定数が増えれば少数政党の候補者が滑り込めると期待できるが、
定数が増えたことで獲得議席が減ってしまうという奇妙な逆転現象が起きてしまっている。
(c)
下線部Dとあるが、両方式による議席配分の結果が同じになるためには、
各党の得票数(A党700票、B党500票、C党300票)がどのように変わればよいのだろうか。定数3、総得票数1500票は変わらないとし、ドント方式による獲得議席数が、ニューマイヤー方式による獲得議席数と同じになるためには、最低で何人の有権者が投票する政党を変えればよいか。次の文中の〔 あ 〕に入る数を答え、〔 い 〕と〔 う 〕にはA、B、Cのいずれかを選び、その文字を答えなさい。
最低で〔 あ 〕人の有権者が投票する政党を〔 い 〕党から〔 う 〕党に変えればよい。
あ―34人 い―A党 う―C党
*ここまで到達するまで一苦労だがラストも難問。
定数3、総得票数が1500票のとき、
ドント方式での結果をニューマイヤー方式の結果と等しくするには、
どの党からどの党に最低何票が流れたらよいか。
【A党;700票 B党;500票 C党;300票】

定数3をみる。
ニューマイヤーではA:B:C=1:1:1
ドント方式ではA:B:C=2:1:0
結果を等しくさせるには、A党を1議席減らしてC党にうつせばよいので
A党からC党への票の移動のみを考えればよい(い―A党、う―C党となる)
@ドント方式でA:B:C=1:1:1を実現する場合@
A党の得票数をX、C党の得票数をYとおくと・・(B党は500票のまま)
| ÷1 | ÷2 | |
| A党 | X | X/2 |
| B党 | 500 | |
| C党 | Y |
ここで、C党にも1議席を獲得させるには、Y>X/2となればよい。
X+500+Y=1500
X+Y=1000
YにX/2を代入して不等式。
X+X/2<1000 (←X/2はYより小さい値なので、X+X/2は1000未満)
3/2X<1000
X<666.66・・
Xが666.66・・票より小さくなれば(整数値でいえばX<666票であれば)
Y>X/2となり、C党に議席が移る。
700-666=34票、最低34票がA党からC党に移動すればよい(あ―34)
ちなみに、
@ニューマイヤー方式でA:B:C=2:1:0を実現する場合@
表3から、
A:1・6/15 B:1 C:9/15
Cの議席を失くして、Aの議席を2つにするには、
C⇒Aに2/15移動させて、A:1・8/15 C:7/15にすればいい。
2/15は票数でいえばいくらか?
3×□/1500=2/15
3×□/1500=200/1500
3×□=200
□=66.66・・
最低でも67人の有権者がCからAに鞍替えしないと、ドント方式と結果が等しくならない。
難問特色検査の解説ページに戻る



コメント