問題ＰＤＦ
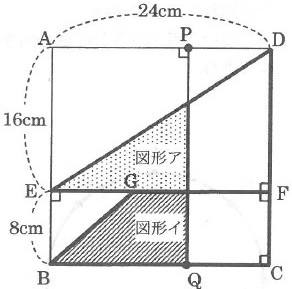
下の図のように、１辺の長さ24ｃｍである正方形ＡＢＣＤがあります。
辺ＡＢ上にＡＥの長さが16ｃｍとなる点Ｅをとり、Ｅを通って辺ＡＢに垂直な直線と辺ＣＤが交わる点をＦとします。また、直線ＥＦの上にＥＧの長さが９ｃｍ、ＧＦの長さが15ｃｍとなる点Ｇをとります。
動く点Ｐ、Ｑがそれぞれ頂点Ａ、Ｂを同時に出発し、点Ｐは辺ＡＤの上を頂点Ｄまで、点Ｑは辺ＢＣの上を頂点Ｃまで、ともに毎秒１ｃｍの速さで進みます。直角三角形ＤＥＦと台形ＧＢＣＦについて、直線ＰＱの左側の部分をそれぞれ図形ア、図形イとするとき、次の各問いに答えなさい。
（１）
２つの点が動き始めてから12秒後の図形アと図形イではどちらの面積が何ｃｍ2大きいですか。
（２）
図形アと図形イの面積が等しくなるのは２つの点が動き始めてから何秒後ですか。
＠解説＠
（１）
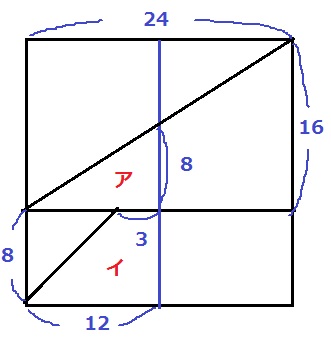
12秒後なので、ＰＱは正方形を縦に真っ二つする。
アの高さは２つの直角三角形の相似から、16×12/24＝８ｃｍ
ア…12×８÷２＝48ｃｍ2
イ…（３＋12）×８÷２＝60ｃｍ2
よって、イの方が12ｃｍ2大きい。
（２）
アとイの数量変化を見極める。
イは長方形に広がっていくが、アは台形で広がっていく。
前問の12秒後から考える。
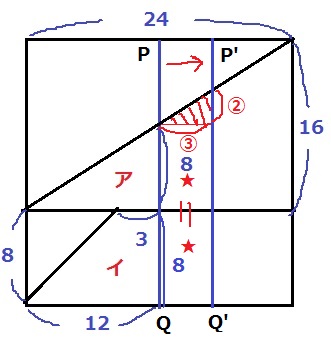
12秒後はともに高さが８ｃｍ。
ＰＱを右にスライドすると、高さ８ｃｍの長方形の面積は等しい。
ということは、赤い斜線がついた直角三角形の部分だけ、アの面積がイより大きくなる。
12秒後でイがアより12ｃｍ2大きくなるので、アとイの面積が等しくなるときは、
赤い斜線の直角三角形が12ｃｍ2になったとき。
直角三角形の横：高さは、24：16＝③：②である。
③×②÷２＝12
③×②＝24
③＝６ｃｍ、②＝４ｃｍのときに等式が成り立つ。
ＰとＱは毎秒１ｃｍ動くので、アとイの面積が等しくなるのは、
12＋６＝18秒後
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント