問題PDF
長さ100cmの2本の軽い棒(棒A、棒B)と、おもりをいくつか用意した。
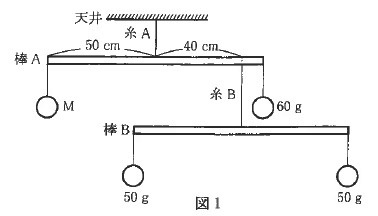
これらを軽い糸を利用し、図1のようにつるしたところ棒は水平となりつり合った。
棒と糸の重さは考えないものとし、以下の問いに答えよ。
問1
糸Bから棒B(おもり2つを含む)をはずし、糸Bに新たなおもりを1つだけつるして
棒Aを水平に保つとしたら、新たなおもりの重さは何gにすればよいか。
問2
おもりMの重さは何gか。
問3
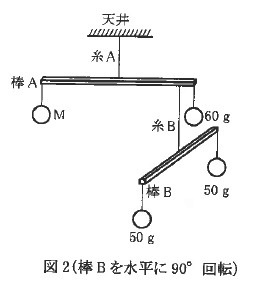
次に図2のように棒Bを水平に保ちながら真上(天井側)から見て90°回転させた。図3は真上から見た棒A、棒Bのようすを表しており、天井からつるした糸Aの位置を黒丸●で示してある。
また50gのおもりをつるした位置を棒Bに白丸○で示してある。
棒Aにつるしたおもり2つをはずし、棒Aに新たなおもりを1つだけつるして棒Aと棒Bを水平に保った。このとき新たなおもりの重さは、おもりMと60gのおもりの重さの和と同じであった。
棒Aのどの位置に何gのおもりをつるしたか。
解答欄の図に、つるした位置をXで描き、Xの近くに新たなおもりの重さが何gか書き入れよ。

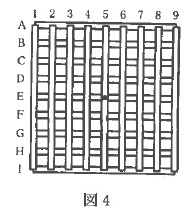
棒をたくさん用いて図4のような格子を作り、棒の交点に名前をつけた。
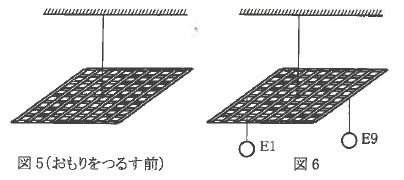
E5を天井からつるすと図5のように格子は水平となりつり合った。
この格子の下側に図6のようにおもりをつるし(洗たく物をつるすイメージ)、
水平になるようつり合わせていく。
ただし、棒の交点(名前のついた点)にのみ、おもりをつるせるものとする。
問4
図5のB9に50g、H9に100gのおもりをそれぞれつるした。
格子を水平にするためおもりを1つだけ使う。
何gのおもりをどの交点につるせばよいか。下図を利用して考えよ。

問5
図5のB6に120g、H9に60gのおもりをそれぞれつるした。
格子を水平にするため100g以下のおもりを1つだけ使う。
何gのおもりをどの交点につるせばよいか。下図を利用して考えよ。

@解説@
縦横のテコ。テコ全体の重さは重心にかかる。

問1:100g
つり合っていた状態から棒B(おもり2つ)を抜くので、
糸Bにつるす代わりのおもりは、つるされていたおもりの合計50+50=100g
糸Bは棒Bの重心に結ばれており、重心には100gの重さがかかっている。
問2:140g
前問より、糸Bには100gのおもりがぶらさがっている。
棒Aのモーメントから、100×40+60×50=M×50
M=140g
問3:後図参照。
新たなおもりの重さは、Mと60gの合計なので、
前問から、140+60=200g


つるす場所も問1と同様に考える。
棒Aと棒Bの交点に100gのおもりをつるしたのと同じなので、
モーメントから、100×4÷200=2
支点から2つ左。
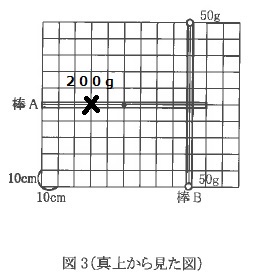 ←解答
←解答
問4:D1、150g
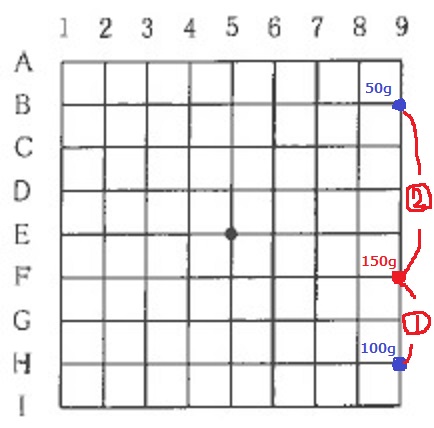
2つのおもりはともに9列にぶら下がるので、9列のみで考える。
おもりの重さの比(1:2)から支点からの距離は逆比→2:1
2つの青点は、支点となるF9の赤点に統合できる。
F9には、50+100=150gの重さがかかる。

てこ全体がつり合うには、正反対に同じ重さのおもりをつるす。
中心点であるE5を通るように、点対称となる点D1に150gをつるせばいい。
問5:G1、90g
前問と同様だが、斜めで考える。
B6とH9を結ぶ。
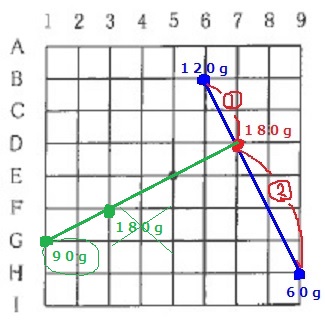
2つの青点は、D7の赤点(180g)に統合できる。
中心点E5を通過する直線をひく。
交点はF3かG1。
F3だと180gとなり、問題文の『100g以下のおもり』に適さない。
よって、G1に90gをつるす。


コメント