2021年度　豊島岡女子学園中学２回目過去問【理科】大問１解説

問題ＰＤＦ
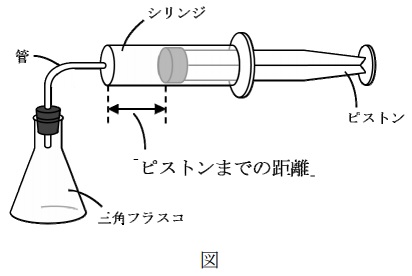
　図のように、三角フラスコと断面積が10ｃｍ²のシリンジを管で繋いだ装置を作りました。シリンジの中のピストンは、なめらかに動かすことができます。図のように、ピストンの位置はシリンジの左端からピストンの先端までの距離（以下、「ピストンまでの距離」と呼ぶことにします）で表すことにします。「ピストンまでの距離」が０ｃｍのとき、装置内の空気の体積は50ｃｍ³でした。装置内の空気の温度は自由に設定し、一定に保つことができるように作られています。

【実験１】
装置内の空気の温度を27℃にしたとき、「ピストンまでの距離」は７ｃｍでした。この状態から装置内の空気の温度を変化させたところ、「ピストンまでの距離」は表１のようになりました。

（１）
装置内の空気の温度を57℃にすると、「ピストンまでの距離」は何ｃｍになるでしょうか。
四捨五入して小数第１位まで答えなさい。

（２）
装置内の空気の温度を変えたところ、装置内の空気の体積は127.2ｃｍ³になりました。
このときの装置内の空気の温度は何℃でしょうか。四捨五入して整数で答えなさい。

　気体の入ったビニール袋を密閉し山に登ると、高度が上がるにつれ袋がふくらむ様子を観察することができます。これは、袋のまわりにある空気が薄くなることで、袋の中の気体の体積が大きくなるためです。このように、気体の体積を変化させる要因には気体の温度のほかにも、気体のまわりにある「空気の濃さ」があります。
「空気の濃さ」は「気圧」という単位を用いて表すことができます。例えば海抜０ｍの地点の「空気の濃さ」はおよそ１気圧であるのに対して、富士山の山頂付近ではおよそ0.63気圧となります。

【実験２】
装置内の空気の温度を27℃に保ち、装置外の「空気の濃さ」を変化させたところ、「ピストンまでの距離」は表２のようになりました。

（３）
【実験２】から分かることとして最も適切なものを選びなさい。
あ：「空気の濃さ」が２倍、３倍になると、「ピストンまでの距離」も２倍、３倍になる。
い：「空気の濃さ」が２倍、３倍になると、「ピストンまでの距離」は1/2倍、1/3倍になる。
う：「空気の濃さ」が２倍、３倍になると、「ピストンまでの距離」は1/4倍、1/6倍になる。
え：「空気の濃さ」が２倍、３倍になると、装置内の空気の体積も２倍、３倍になる。
お：「空気の濃さ」が２倍、３倍になると、装置内の空気の体積は1/2倍、1/3倍になる。
か：「空気の濃さ」が２倍、３倍になると、装置内の空気の体積は1/4倍、1/6倍になる。

（４）
装置外の「空気の濃さ」が0.6気圧のとき、「ピストンまでの距離」は何ｃｍになるでしょうか。
四捨五入して整数で答えなさい。

（５）
装置外の「空気の濃さ」を0.8気圧、装置内の空気の温度を87℃にすると、
「ピストンまでの距離」は何ｃｍになるでしょうか。四捨五入して整数で答えなさい。
ただし、【実験１】は装置外の「空気の濃さ」を１気圧にして行ったものとします。

＠解説＠
（１）8.2ｃｍ
温度を上げると、空気が膨張してピストンを押す。

差を確認する。15℃の差で0.6ｃｍ離れる（比例）
57－42＝15℃
57℃は42℃と72℃の真ん中である。

（２）45℃
ピストンまでの距離が０ｃｍのとき、空気の体積は50ｃｍ³
膨張した空気の体積は127.2－50＝77.2ｃｍ³
シリンジの断面積は10ｃｍ²
【膨張した空気の体積＝断面積×ピストンまでの距離】
ピストンまでの距離は、77.2÷10＝7.72ｃｍ

42＋15×0.12/0.6
＝42＋３
＝45℃

（３）お
空気の濃さ（気圧）とピストンまでの距離は比例でも反比例でもない。

気圧の変化で変わるのは空気の体積。
0.5気圧の空気の体積は、10ｃｍ²×19ｃｍ＋50ｃｍ³＝240ｃｍ³
0.8気圧の空気の体積は、10×10＋50＝150ｃｍ³
同様に計算すると、うえのようになる。
気圧と空気の体積の関係は反比例である。

（４）15ｃｍ

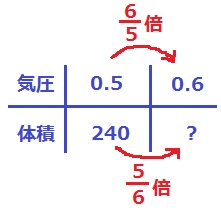
気圧が６/５倍。体積は反比例だから５/６倍。
0.6気圧の空気の体積は、240×５/６＝200ｃｍ³
膨張した空気は、200－50＝150ｃｍ³
再掲【膨張した体積＝断面積×ピストンまでの距離】
ピストンまでの距離は、150ｃｍ³÷10ｃｍ²＝15ｃｍ

（５）13ｃｍ

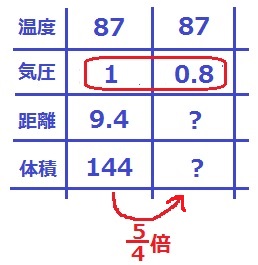
87℃・１気圧の空気の体積は、50＋10×9.4＝144ｃｍ³
１気圧→0.8気圧は４/５倍だから、
0.8気圧の空気の体積は、144×５/４＝180ｃｍ³
ピストンまでの距離は、（180－50）÷10＝13ｃｍ

＠ボイル・シャルルの法則＠
実験２のように、温度（Ｔ）が一定の場合、体積（Ｖ）は圧力（Ｐ）に反比例することをボイルの法則といいます。圧力を上げると空気がグッと押されるので、感覚的に体積は小さくなるとわかりますよね。
また、実験１のように、圧力（Ｐ）が一定の場合、体積（Ｖ）は温度（Ｔ）に比例することをシャルルの法則といいます。温度を上げると空気は膨張して体積が増えます。

ボイルの法則から、反比例の積は常に比例定数で等しいので、
【ＰＶ＝一定】
シャルルの法則より、これも比例定数が一定の値であるのを利用すると、
【Ｖ/Ｔ＝一定】

まとめると・・

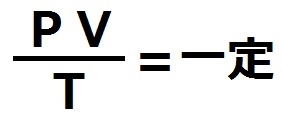
圧力（Ｐ）と体積（Ｖ）の積を温度（Ｔ）で割った値は常に一定となる。
これをボイル・シャルルの法則といいます。
ちなみに温度（Ｔ）は日常で用いられるセ氏温度（℃）ではなく、絶対温度（Ｋ）を使います。

さらに、分子の個数ｎ（モルという物質量が単位）と気体定数Ｒを用いて発展させたのが、
理想気体の状態方程式【ＰＶ＝ｎＲＴ】
すべての気体は温度と圧力が同じである場合、同じ体積に含まれる分子の数は、
気体の種類に関係なく同じであるとするアボガドロの法則に従います。
詳細は高校化学で習います。
難関中学（理科）解説ページに戻る