問題PDF
電気について次の文章を読み、問いに答えなさい。
問題1
ひろし君の家の階段には電球が1つ付いています。1階のスイッチを入れたり切ったりすると、電球がついたり消えたりします。2階にあるスイッチを入れたり切ったりしても電球がついたり消えたりします。これはどんな回路になっているのだろう、とひろし君は考えました。
ふつうのスイッチは図1のようになっています。破線の中がスイッチで、〇印を端子と言います。端子には導線をつなげるようになっています。一方、図2は切り替えスイッチというもので、端子が3つあり、端子の1番と2番がつながっている状態から切り替えると、3番と2番がつながった状態になります。
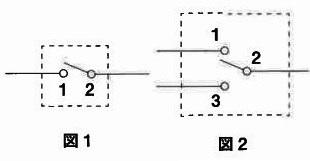
ひろし君はこの2種類のスイッチを使って階段の電球の回路を4つ考えました。
問1
次の回路図のうち、上の文章の下線部のようにはたらくものを選びなさい。

ひろし君は、もし3階建ての家だったらどうしたらいいかなあと考えました。階段に電球が1つだけあり、1階のスイッチでも2階のスイッチでも3階のスイッチでも電球がついたり消えたりするようにしたいのです。どうしてもうまくいかないのでお姉さんのまいさんに助けを求めました。
まい「そうねえ。4路スイッチというのを使うといいよ」
ひろし「それは何?」
まい「そうね。4路スイッチには図3のように4つの端子があって、初めは1番と2番、3番と4番がつながって
いるの。そこでスイッチのつまみを時計回りに90°まわすと、今度は1番と3番、2番と4番がつながるの」
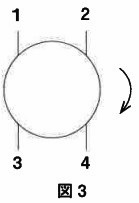
ひろし「90°ずつ2回まわすと元にもどるんだね。スイッチの中はどういうしくみになってるの」
まい「それは考えなさいよ」
ひろし君は4路スイッチの中身(つまみとともに回転する部分)を5通り考えてみました。下のア~オです。点線の円の内部が90°ずつ回転します。
アはななめの2本の線が立体交差していて、ななめの線どうしはつながっていないことを表しています。イは2本のななめの線がつながっていることを表しています。

問2
上のア~オのうち4路スイッチとしてはたらくものを選びなさい。
まい「スイッチの中はわかったね。
じゃあ、この4路スイッチを使って、3階建て用の回路をかいてみて」
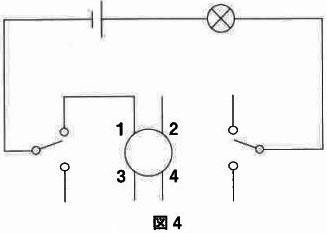
問3
図4には電池1個、豆電球1個、切り替えスイッチ2個、4路スイッチ1個がかいてあります。これらをつないで、どのスイッチでも豆電球をつけたり消したりできるようにするには、どのようにつなげればよいでしょうか。下のなかから選びなさい。

問題2
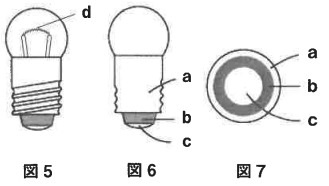
図5は豆電球です。ソケットに入れる前の豆電球はこんな形をしています。以下では図6のように簡単にかきます。図7はそれを下から見た図です。図6と図7で、aは金属でできていて、ねじのようになっている部分です。bは黒くて電気を通さない物質でできています。cも金属でできています。
ひろし「ソケットを使わないで豆電球と乾電池をつないでみよう。
つなぎ方によっては豆電球がつかないこともあるね。なんでかなあ」
まい「豆電球の中にはフィラメントという細い金属の線(図5のd)があって、そこを電球が流れると光るのよ。
電流がフィラメントを通らないようなつなぎ方だと豆電球はつかないの」
問4
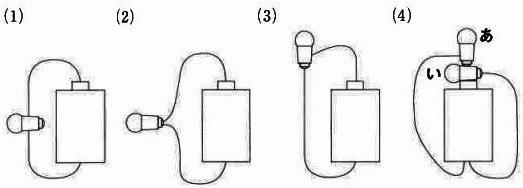
豆電球と乾電池と導線を次の(1)から(4)のようにつなぐとき、豆電球がつくものにはA、つかないものにはBと書きなさい。(4)は、あ、いのそれぞれの豆電球について答えなさい。
問5
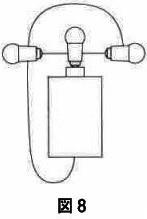
図8の回路について回路図をかくと、下のア~コのどれになりますか。
乾電池の記号は線が長い方が+極です。

図6のbの部分は電気を通さない物質でできています。
ひろし君はこのことを不思議に思いました。
ひろし「bの部分を金属に変えた豆電球を作るとどうなるかなあ」
まい「ひろしが考えている豆電球を作るのはむずかしいから、ふつうの豆電球を2個つないで、
片方の豆電球だけaとcを直接つなぐといいよ」
問6
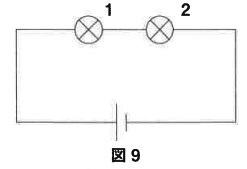
ふつうの豆電球1と2を図9のように直列にして乾電池1個をつなぐと2つとも同じ明るさでつきました。ここで豆電球1について図6のaとcをアルミホイルでつなぐと豆電球1と2はそれぞれどうなりますか。次のなかから1つずつ選びなさい。
ア:一瞬明るくかがやいてすぐ消える
イ:はじめよりも明るくつく
ウ:はじめと同じ明るさでつく
エ:はじめより暗くつく
オ:消える
問題3
ひろし君は豆電球と電流計と電源装置をつないで豆電球の明るさを調べてます。電源装置は図10のようなもので、つまみを回すと1.6V、1.7Vのように細かく電圧を変えることができます。以下では電源と言います。
実験1
はじめに、図11のように豆電球1個と電流計をつないだ回路を作って、回路の+を電源の+に、回路の-を電源の-につなぎます。このあとで登場する回路でも同じようにします。電源のつまみを回すと電圧が変化して、そのとき豆電球を流れる電流を電流計で測ることができます。また豆電球の明るさも観察します。このあとも同じ種類の豆電球を使うこととします。
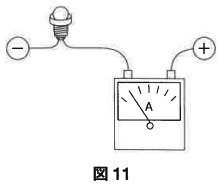
結果は表1のようになりました。たとえば「かすかにつく」はその電圧や電流になったとき、初めてかすかについたという意味です。ほかの明るさについても、初めてその明るさになったときの電圧や電流を表しています。空らんは上と同じ明るさという意味です。
「まぶしい」ときより電圧を高くすると豆電球が切れる心配があるので、ここで実験をやめました。表の2.6Vのところの×は実験を行わなかったことを示します。これからも「まぶしい」をこえるような実験は行わないことにします。

ひろし君は考えました。「電流がたくさん流れるほど豆電球が明るくなるんだ」
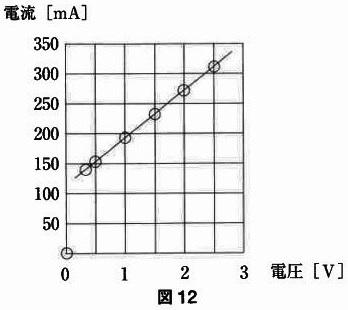
グラフにすると図12のようになりました。
実験2
次に、図13のように豆電球2個を直列につなぎ、それに電流計をつないだ回路を作って、電流計はAの記号で表します。
このとき、豆電球1を流れる電流と豆電球2を流れる電流は同じです。この電流を電流計で測ることができます。実験はいろいろな電圧について行いましたが、表2には3Vの場合だけあげておきます。

ひろし君は考えました。「電源の電圧が3Vのときに電圧計で豆電球1個の電圧を測ったら1.5Vになると思う。実験1でも実験2でも1.5Vのときは230mA流れてふつうの明かるさだ。直列のとき電圧は足し算になっているんだ」
実験3
次に、図14のように豆電球2個を並列につなぎ、それに電流計をつないだ回路を作って測りました。豆電球1を流れる電流と豆電球2を流れる電流の合計を電流計で測ることができます。実験はいろいろな電圧について行いましたが、表3には1.5Vの場合だけあげておきます。

ひろし君は考えました。「電源の電圧が1.5Vのときは豆電球1個には実験1と同じように230mAの電流が流れてふつうの明るさになる。2つの豆電球の電流が合わさって、電流計は460mAになるんだと思う。並列のときは電流が足し算になっているんだ」
実験4
最後に、図15のように豆電球3個と切り替えスイッチと電流計をつないだ回路を作りました。
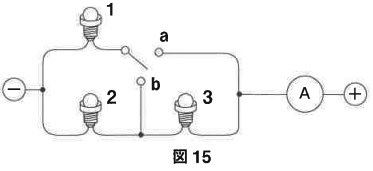
問7
切り替えスイッチをaにつないで、電源の電圧を上げていきます。豆電球1が初めて「まぶしい」になったとき、電圧を上げるのをやめます。このとき、豆電球3の明るさはどうなっていますか。下の表にしたがって番号または記号で答えなさい。

問8
電源の電圧を問7のままにして、切り替えスイッチをbにつなぐと、豆電球1と3の明るさはどうなりますか。問7と同じように答えなさい。
@解説@
問1:エ
1階と2階の電源スイッチで使われる3路スイッチ。類題経験者は多いと思われる。

ア:一方のスイッチがOFFだと、他方をONしても付かない。
イ:一方のスイッチがONだと、他方をOFFしても付いたまま。
ウ:一方が下にあると、他方を上に切り替えても付かない。
問2:オ
4路スイッチ。
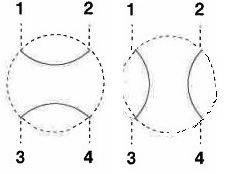
『初めは1番と2番、3番と4番がつながっている。
スイッチのつまみを時計回りに90°まわすと、1番と3番、2番と4番がつながる』
他の選択肢と形が異なる回路で躊躇するが、オが正答。
問3:イ
頭がこんがらがってくる(´д`)

『1―3、2―4』がつながっている状態を考えると、
アとウでは右と左で回路が分断されてしまう。
左右の3路スイッチをONにしても豆電球はつかない。
『1―2、3―4』がつながっている状態を考えると、
エでは上下で回路が分断されるので、同様に×!
イで2通りを試してみよう。分断されない。
問4:①B②B③A④あAいA
ソケットなしで豆電球をつける。
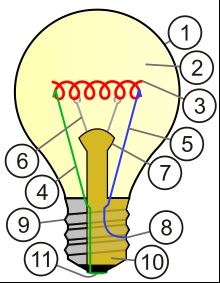 ¥
¥
wikiより。豆電球の中身。
フィラメントに電流が通らないと豆電球はつかない。
下と横をつなげるとフィラメントに電流が通って光る。

(1)(2)のようにつなげると、抵抗であるフィラメントを回避して電流が流れるので、
フィラメントに電流がいかず、豆電球がつかない。
発光ダイオードのように向きは決まっていないので、(4)は双方つく。
ちなみにフィラメントは融点の高いタングステン(元素記号;W)が使われる。
問5:カ
10択もあり、紛らわしい選択肢も多くて難しい。
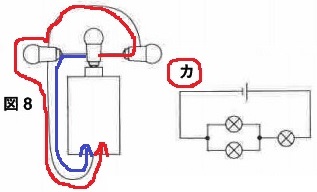
電池の+から出発。最初の電球を通過後、左右に分岐する。
青ルートは1つの豆電球を通って-へ。
赤ルートでは2つの豆電球を通りそうだが、1つしか通らない!
前問の(1)と同じで、ソケットがない状態で横と横をつなぐと、
フィメラントに赤ルートの電流は流れない。カの回路図になる。
問6:豆電球1―オ、豆電球2―イ
豆電球1はフィラメントを避けるように電流が流れるので消える。
直列につないだ豆電球が2つから1つに減るのと同じで、豆電球2は明るくなる。
問7:2
最後の2題はかなり悩みました(*_*)
豆電球の明るさはW(ワット)で決まるので電圧V×電流A=Wかなと思いきや、、

よくみたら電流と電圧が比例になっていない!
0.5Vあたり40mAで増加しているものの、0.3V-136mAと0V-0mAは直線上にない。
勝手にオームの法則で計算しちゃダメなんですね。
ひろし君も『電流がたくさん流れるほど豆電球が明るくなるんだ』と電圧には言及していません。
豆電球の明るさはあくまで電流に依存し、表1の電圧―電流―明るさの対応表から解答します。
解答で使える範囲は問題文で提示された実験結果のみ。
〔ふつうの明かるさ〕で比較すると、
豆電球1個→1.5V・230mA
直列2個→3V・230mA
(直列は電圧が足し算;3V=1.5V+1.5V。電流は等しい)
並列2個→1.5V・460mA
(並列は電流が足し算;460mA=230mA+230mA。電圧は等しい)
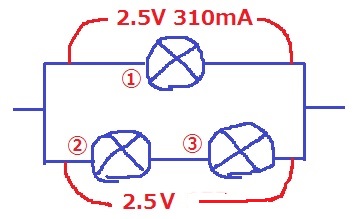
豆電球1が〔まぶしい〕ので、豆電球1には310mAの電流が流れている。
表1は豆電球1個分の話。豆電球1は並列1個なので、2.5Vの電圧がかかっている。
並列の電圧は等しいので、豆電球2と3は合わせて2.5Vの電圧。
直列の電圧は和になるから、豆電球3単独では1.25V。
表1より、1.25Vに対応する明るさは〔暗い〕
問8:豆電球1―0、豆電球3―4

電源は2.5Vを維持する→回路全体では2.5Vの電圧がかかっている。
並列は電流が足し算だから、豆電球1と豆電球3を流れる電流量は①:②
つまり、電流(mA)①と②に対応する電圧の和が2.5Vとなるときの①と②の電流量を考える。
表を見ると、電流量が半分になると豆電球の明るさにだいぶ差ができる。
豆電球3の電圧は2.5V未満なので〔まぶしい〕ではないが、仮に豆電球3を2.5Vで計算すると、
豆電球1の電流は310÷2=155mAで、〔かすかにつく〕のギリ上にあたる。
試しに、豆電球1を〔かすかにつく〕で最も小さい0.5V・150mAで計算すると、
豆電球3の電流は150×2=300mAとなるが、電圧は2.5-0.5=2.0Vで
表1から2.0Vの電流は270mAだからつじつまが合わない。
電圧を上げると電流は増えるので、豆電球1の電圧をさらに上げて計算しても合わない。
豆電球1は0.5V未満の電圧で〔つかない〕になる。
今度は、豆電球3を〔とても明るい〕で最も小さい2.0V・270mAで計算すると、
豆電球1の電流は270÷2=135mAで〔つかない〕
豆電球1の電圧は0.3V未満だから、豆電球3は2.5-0.3=2.2Vを超える。
実際の電流量は270mAを超えることになり、豆電球3は〔とても明るい〕になる。


コメント