問題PDF
下の図において、四角形ABCDは平行四辺形で、
DE:EC=1:4、CF:FG=1:1、AGとHFは平行です。
次の比をもっとも簡単な整数の比で表しなさい。
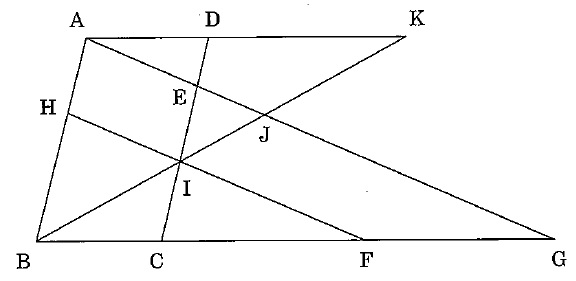
(1)BC:CG
(2)AD:DK
(3)AE:EJ:JG
(4)四角形ABCDの面積:三角形EIJの面積
@解説@
(1)

△ADE∽△GCE(∽…相似)
DE:CE=①:④より、AD:GC=□1:□4
平行四辺形ABCDから、AD=BC=□1
BC:CG=1:4
(2)

AG//HFを頼りに、△CFI∽△CGE
CF:FG=CI:IE=1:1(IはCEの中点)
CI=IE=②
△BCI∽△KDIより、
DK=□1×③/②=□3/2
AD:DK=1:3/2=2:3
(3)

下準備として先に比を統一しておく。
先ほどAD:DK=2:3と出したので、□1を2倍して②にチェンジ。
△AJK∽GJBより、AJ:GJ=AK:GB=⑤:⑩=1:2

連比処理。
AJ:JG=1:2
AE:EG=1:4 ←(1)の∽
⑤と□3を最小公倍数△15で統一して、
AE:EJ:JG=3:2:15
(4)
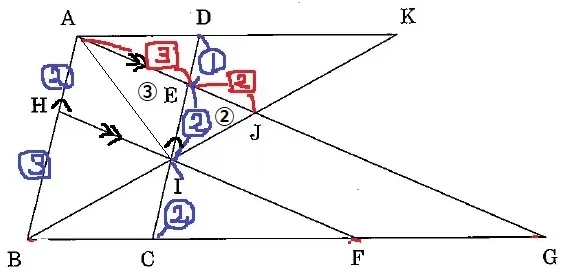
△EIJ:△EIA=JE:EA=②:③
上底+下底の和から面積比を求める。
平行四辺形ABCD=△EIJ(③)×⑩/②=⑮
したがって、四角形ABCD:三角EIJ=15:2



コメント