問題PDF
固形セッケンは同じ体積のとても小さな棒状のもの(以下、A)が集まってできています。
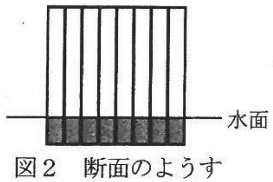
少量のセッケンを水にとかし、水のはいった水そうにたらすと、Aが図1、2のように水面に集まり、
1層のセッケンまくをつくることが知られています。
これはAの一方のはしが水になじみやすい性質をもっていて、
反対側のはしが水になじまない性質を持っているためです。

問1
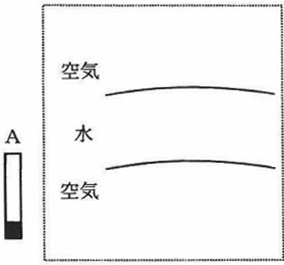
セッケン水でシャボン玉をつくった時の断面のようすを、解答らんの図に、
図2のようにAを書き込み、完成させなさい。
ただし、大きさは解答らんのAの図を参考にしなさい。

 ←解答欄
←解答欄
固形セッケン1cm3を水にとかして水よう液を1000cm3とし、よく混ぜて均一にしました。
このセッケン水を図3のような目盛りの付いた細いガラス管で吸いとって、
10てきで何cm3になるかを測定しました。
測定の結果、セッケン水10てきの体積は0.2cm3でした。

問2
セッケン水1てきにとけているセッケンの量を固形セッケンの体積として求めると、
何cm3であったといえますか。計算して答えなさい。
セッケンが水面にまくをつくる性質を用いて、
セッケンまくの体積と面積からAの長さを調べてみましょう。
まず水そうに水を入れ、水面にうすくチョークの粉をうかべました。
次に、目盛りの付いた細いガラス管を用いてセッケン水を1てきたらしました。
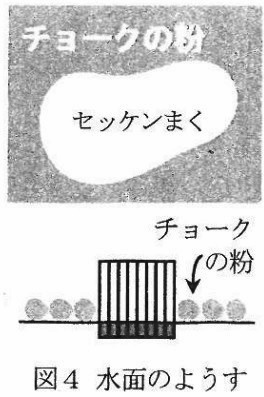
するとセッケン水の中のAが集まってセッケンまくが図1のように1層になってうかび、
チョークの粉をおしのけて図4のように広がりました。
水面に上から方眼紙をかぶせ、しばらくしてから方眼紙を引き上げると、
方眼紙にはチョークの粉がついた部分とついていない部分ができ、
水面のセッケンまくと同じ形を写し取ることができました。
写し取った方眼紙をかわかして、セッケンまくの面積を求めてみましょう。
問3
実験前に実験器具の水洗いをしたため、ガラス管の内側に水てきがついていました。
この場合はセッケン水を吸い上げて捨て、ガラス管の内側にセッケン水でぬらすと、
誤差の小さい、より正確な測定ができます。それはなぜですか。理由を答えなさい。
問4
1辺1cmの方眼紙を用いてセッケンまくのかたちを写し取ると、
セッケンまくしかついていないマス目(下図の〇)と、
セッケンまくとチョークの粉がともについているマス目(下図の▲)がありました。
マス目を数えて面積を求めるときに、実際の面積に近い値になると考えられる計算方法として
最も適当なものを選び、理由も答えなさい。

ア:(〇のマスの数)×1cm2
イ:(〇のマスの数)×1cm2+(▲のマスの数)×1cm2
ウ:(〇のマスの数)×1cm2+(▲のマスの数)×0.5cm2
問5
チョークの粉がついていないセッケンまくの面積は、100cm2でした。
セッケンまくの厚みは何ナノメートル(nm)ですか。
ただし、セッケンまくの体積は問2で求めた体積と同じだとします。
また、ミリメートルよりも小さなものの長さを表すときに用いる
マイクロメートル(μm)とナノメートル(nm)の単位には次のような関係があります。
1mm=1000μm 1μm=1000nm
問6
Aはおもに炭のもととなる小さなつぶがおよそ決まった個数、下図のようにすき間なく並んでできています。
1つのAは、この小さなつぶが20個程度結びついてできているとすると、
小さなつぶの1個の大きさはおよそどの程度ですか。もっとも近いものを、次のなかから選びなさい。

ア:0.00001nm イ:0.001nm ウ:0.1nm エ:10nm オ:1000nm
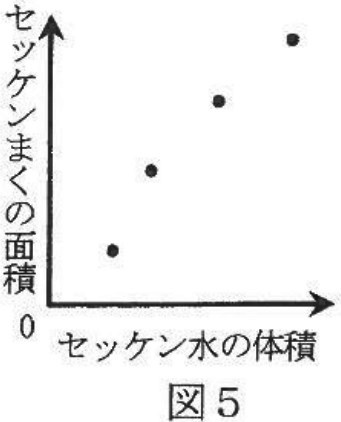
最後に、セッケンまくをつくるために水面にたらすセッケン水の量を少しずつ多くしながら4回実験を行いました。これらの実験の結果は図5のようになりました。
問7
「セッケン水の体積」と「セッケンまくの面積」にはどのような関係があると考えればよいでしょうか。本来あるべき性質を示したグラフとして最も適当なものを選びなさい。

@解説@
Aの正体はセッケンや洗剤に含まれる界面活性剤。
水になじみやすい親水性と水になじみにくい疎水性(油になじむ)という2つの特徴をあわせもち、
本来、混ざることのない水と油を結びつけて、水で油汚れを落とすことができる。
問1:下図参照。
シャボン玉をつくったときの界面活性剤を図示する。
水になじむ黒い部分が水に接着する。

↑汚い図で申し訳ない。マウスの手ブレです。
シャボンの内側と外側の表面に界面活性剤が並ぶことで、
小さく縮こまろうとする水の表面張力を抑え、シャボン玉ができる。
長さは左のAを参照。
本数はたくさんあった方が、図2の通り、現実に即している。
問2:0.00002cm3
10てきのセッケン水が0.2cm3なので、
1てきのセッケン水は0.2÷10=0.02cm3
一方で、セッケン水(水溶液)は1000cm3のうち固形セッケンは1cm3
濃度は0.1%
セッケン水1てきに溶けているセッケンの体積は、
0.02×0.1%=0.00002cm3
問3:ガラス管内のセッケン水が水で薄まらないため。
セッケン水をたらすガラス管を水で洗ってしまうと、
セッケン水の濃度が薄まってしまう。
セッケン水が薄まるとセッケンまくの面積の誤差も大きくなる。
実験に使用する溶液で器具を洗うことを共洗いという。
問4:ウ、▲のマスの平均面積がおよそ0.5cm2と考えられるから。
写真では一部しか写っていないので▲の平均面積が0.5cm2になるかはわからないが、
▲マスを全て考慮しないアと、▲マスをすべて1cm2と考えてしまうイと比べると、
最も適当なのはウとなる。
問5:2nm
セッケンまくの体積は0.00002cm3、表面積は100cm2
Aの高さは、
0.00002÷100
=0.0000002cm
=0.000002mm
=0.002μm
=2nm
ケタミス注意!ミリ→マイクロ→ナノは3桁ずつズレる(ナノの下はピコ)
高校にあがると有効数字を使い、2.0×10-7と表すこともある。
問6:ウ
ここも前問を利用する。
Aの長さは2nmで20個のつぶで厚生されることから、
つぶ1つの長さ(直径)は2÷20=0.1nm
問7:ア

点線をたどっていくとオっぽくなるが、
グラフ上の相関関係は近似値を直線でひく。
決して折れ線にしないこと!理由は測定値は誤差を含んでいるため。


コメント