問題ＰＤＦ
太陽が東から昇り西に沈むのは、地球が西から東へ回転しているからです。
地球のこの動きを自転と呼びます。
しかし西から昇る太陽を見ることは可能です。
例えば地球の自転よりも速く西へ向かって移動すれば、
太陽が西から昇ってくるのを見られます。
問１
地球を一周の長さが40000ｋｍの球として、地球の赤道上を西へ、
時速何ｋｍより速く移動すれば、西から昇る太陽が見られますか。
小数第１位を四捨五入して整数で答えなさい。
問２
時速800ｋｍで飛ぶ飛行機で赤道上を西へ飛べば、
飛行機の中から太陽の動きはどのように見えますか。
下のア～ウとエ～カからそれぞれ１つずつ適するものを選びなさい。
ア：太陽は東から昇る。 イ：太陽は西から昇る。 ウ：太陽の高さは変わらない。
エ：昼間の長さは通常のおよそ半分になる。
オ：昼間の長さは通常のおよそ２倍になる。
カ：昼間の長さは通常と変わらない。
地球が丸いため、東の土地ほど日の出が早く見られます。
しかし日本（離島をのぞく）でお正月の初日の出が最も早く見られる場所は、
最も東の場所ではなく、富士山山頂です。
これも地球が丸いため、山の高いところほど太陽の光が早く当たるからです。
このことを利用すると、高い場所から低い場所へ急速に降りることにより
日の出が二回見られることになります。
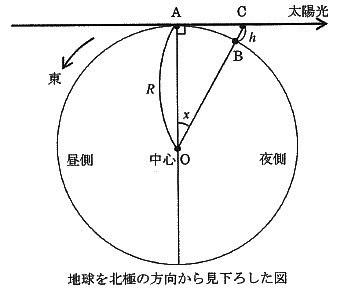
上の図で、Ａ地点は太陽の光が当たりちょうど日の出を迎えています。
場所は赤道上とし、時期は春分か秋分の日とします。
西側のＢ地点ではまだ日の出になりませんが、高さｈのＣ点では太陽の光が来ています。
この状態から地球が角度ｘだけ東へ自転すると、Ｂ地点でも日の出になります。
問３
Ｃ点の高さｈを10ｍ（＝0.01ｋｍ）、地球の半径Ｒを6400ｋｍとします。
ＡＣの距離はおよそ何ｋｍですか。次のなかから最も適するものを選びなさい。
ただし下に示した三辺の長さがａ、ｂ、ｃの直角三角形では、
ａ×ａ＋ｂ×ｂ＝ｃ×ｃの関係がなりたちます。
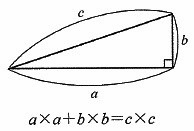
問４
Ｃ点に太陽の光が当たってから、Ｂ地点に太陽の光が当たるまで、何秒かかりますか。
小数第１位を四捨五入し、整数で答えなさい。
ただし、地球の半径Ｒに対してｈが十分に小さいので、
ＡＣの長さがＡＢの長さと同じとみなしてかまいません。
この時間内にＣからＢへ10ｍ降りれば、Ｃで日の出を見た人が二回目の日の出の瞬間を見られます。これとは逆に、日没直後に高いところに登って行くと、西から昇る太陽を短時間でも見ることができます。
＠解説＠
立式はそれほど苦労しないが、計算がヤバイ( ;∀;)
そこまでして初日の出みたいか？
問１：時速1667ｋｍ
地球の自転速度より速く西に走れば、西から昇る太陽を見られる。
地球の自転速度は、40000÷24＝1666.66…→時速1667ｋｍ
問２：ア・オ
地球の自転速度より遅いので太陽は通常通り東から昇る→ア
夜から逃げるように移動するので昼間の長さは長くなる→オ
自転速度の半分弱で西に移動するので、昼間の長さはおよそ２倍。
問３：ウ
△ＡＯＣで三平方の定理を使うだけ。
小学生は習わないので、公式が与えられている。
計算が面倒くさいョ(;´Д｀)
ＡＣ×ＡＣ
＝6400.01×6400.01－6400×6400
＝40960128.0001－40960000…
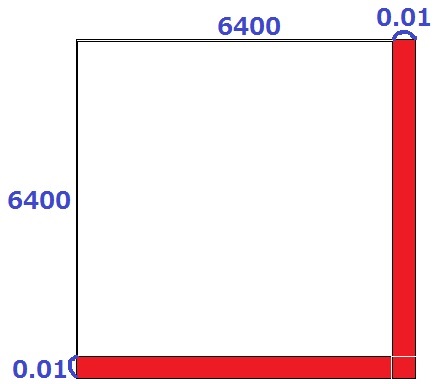
うえの図のように考える。
１辺が6400.01の正方形から、１辺が6400の正方形をひく。
赤い部分の面積が答えになる。
6400×0.01×２＋0.01×0.01
＝128＋0.001
＝＝128.0001
11×11＝121なので、ＡＣは11ちょい上→ウ
問４：24秒
ＡＢに線分をひく。
前問より、ＡＣ＝ＡＢ＝１１ｋｍ。
弦が11ｋｍとなる中心角ｘを利用して、１日を案分する。
２４（時間）×3600（秒）×11ｋｍ/40000ｋｍ（円周）
＝23.76→24秒
24秒以内に10ｍの丘を下れば、２度目の日の出を見ることができる。
やればできる時間なので、ぜひお試しください。。
難関中学（理科）解説ページに戻る
コメント