問題PDF
みさなんが学校などで使用する温度計の多くは、温度によって体積が変化する液体を利用した液体温度計です。一方、金属の体積変化を利用した温度計もあり、この温度計ではバイメタルという金属が使われています。
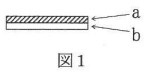
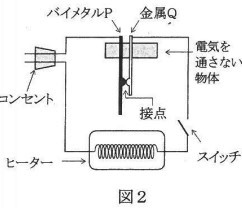
バイメタルとは、図1のように体積が変化しやすい金属aと体積が変化しにくい金属bをくっつけたもののことをいいます。金属aのみ、または金属bのみをあたためると、それ自体が曲がるなどの変形はほとんどせず、長さだけが伸びます。しかし、図1のバイメタルをあたためると、金属どうしは離れずに、バイメタル全体が曲がります。このようなバイメタルは図2のような回路で、ドライヤーやこたつなどにも使用されています。ただし、図2のバイメタルPと金属Qは、通常は接点で触れていますが、離れることもできます。また、バイメタルPと金属Qの上部は電気を通さない物体によって固定されています。
(1)
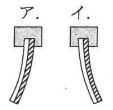
図1のバイメタルの端を固定してあたためます。
このときのバイメタルの曲がり方として正しいものを選びなさい。
(2)
ドライヤーやこたつで、図2の回路を使うとき、
バイメタルPはどのような役割を果たすか答えなさい。
続いて、図3のような形のバイメタルを使用する場合を考えます。
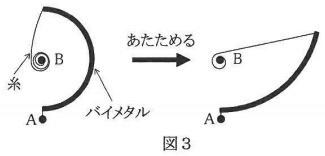
図3では、バイメタルの一端がAに固定され、もう一方の端は糸に接続し、その糸は回転することのできるBに取り付けられています。このバイメタル部分の温度が変わると、バイメタルは糸を引き、Bが回転します。
(3)
バイメタルをあたためて図3のように変形させるためには、どの部分を金属a、bにすればよいですか。最も適当なものを選びなさい。

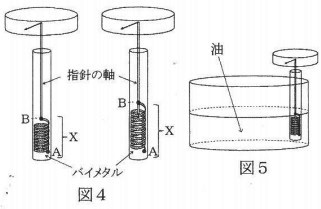
このように、バイメタルによる回転を利用すると、温度計をつくることができます。実際の温度計内では、図4のように、バイメタルの一端をAでケースを固定し、もう一方の端を指針の回転軸Bに取り付けます。バイメタルをたくさん巻いているのは、小さな温度変化でも指針の回転する角度を増やして、より精度よく温度を測るためです。ただし、①Xの部分の長さは図4の左側のように短くし、右側のように長くしません。また、熱した油の温度を調べるときは、図5のように先端を入れて温度を測ります。
(4)
下線部①について、Xの部分を長くしすぎた場合、熱した油の温度を測定すると、
どのような問題が生じると考えられるか説明しなさい。
次に、物体の体積変化とは違った現象を利用した、白金抵抗温度計について考えます。白金抵抗温度計は、金属の一種である白金(プラチナ)に電気を流すことで温度を調べる温度計です。その仕組みを調べるために、次のような実験を行いました。以下の実験で用いる、mAという単位は、ミリアンペアと読み、1000mAは1Aと等しいです。
実験1
図6のような回路を組み、温度0℃の白金1個をあたためていったときの温度と電流の関係を調べた。その結果の一部は、表1のようになった。

実験2
同じ形、同じ体積の白金をたくさん用意した。まず、図7のように2個の白金を直列につないだときの電流を調べた。次に、白金の個数を3個、4個と直列に増やしていったときの電流も調べた。このような実験を、すべての白金を0℃にして行った場合と50℃にして行った場合の結果の一部は、表2のようになった。
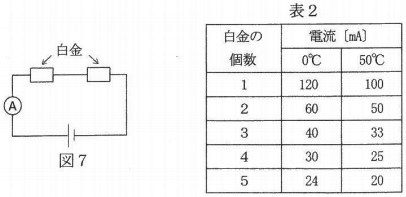
実験1から白金の温度を高くすると電流は小さくなることがわかります。また、実験2からそれぞれの温度で白金の個数を増やすほどに電流が小さくなっていくことがわかります。これらのことから②温度0℃の白金を( あ )個直列につないだときと、温度125℃の白金を( い )個直列につないだときの電流が等しくなることがわかります。
(5)
下線部②について、( あ )( い )に入る整数の組み合わせを1つ答えなさい。
実験3
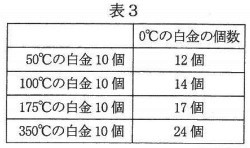
白金を10個直列につなぎ、この白金をあたためていったときの電流を調べた。この結果と、実験2の結果を見比べると、電流の大きさが等しくなる組み合わせがみつかった。そのうちのいくつかをまとめると、表3のようになった。
(6)
温度350℃の白金1個で電流を調べたときは何mAになるか答えなさい。
実験3より、あたためた白金と同じ電流になるような0℃の白金の個数は、規則的に変化することがわかります。また、温度を0℃より下げた場合も同じ規則で0℃の白金の個数は変化しました。
(7)
温度0℃のときの電流と比べ、同じ白金の個数で、電流の大きさが半分になるような温度は何℃か答えなさい。
この実験からわかるように、白金の温度を調べれば白金に流れる電流が計算できます。白金抵抗温度計では逆に、白金を流れる電流の大きさを調べることで白金の温度を計算します。このように、「温度とともに何かが規則的に変化する」という物体の性質を利用してさまざまな温度計がつくられています。それぞれの種類の温度計には長所、短所があり、それぞれに適した場面で使用されています。
(8)
白金抵抗温度計は-200℃程の非常に低い温度でもよく利用されます。
一方で液体温度計はそのような温度では使用されません。その理由を答えなさい。
(9)
実験1~3で使った白金1個を白金抵抗温度計として用いた場合を考えます。
この白金に流れる電流が300mAだった場合、白金温度計は何℃を示すか答えなさい。
@解説@
(1)ア


金属aは変化しやすい、金属bは変化しにくい。
温めると金属aが大きく膨張し、aの長さが長くなる。
距離の長いアウトコースがaとなる。
(2)温度が上昇すると自動的に電気が切れて、温度を一定に保つ。
*バイメタルは授業でも扱うので書きやすかったと思う。
《バイ》は「2つ」を意味する接頭語。
(3)エ


効果的に糸を引くには、膨張率の大きいaは長くとった方が良い。(ア・イ×)
ウとエを比較したとき、ウの方がaの距離は長くなるが、
アーチの外側から内側にあるbを引っ張らなくてはならなくなり、
膨張してaが伸びようとしても、あまり膨張しないbに引っ張られる方が大きくなる。
エのように、アーチの内側からaがbをグッと押す形で糸をグッと引っ張る。
(4)バイメタルの上部が油の表面から出てしまい、適切な温度を計測できない。
*らせん状のところにバイメタルがある。
らせんを長くすると、油に浸かるバイメタルと浸からないバイメタルがでてしまうので、
温度計の役割が果たせなくなる。
(5)あ:3、い:2


表1:温度を高くすると電流は流れにくくなる。
表2:直列の個数を増やしていくと、電流量は白金の数で割った値(個数と電流量は反比例)
1個あたり、0℃の白金は120mAで、125℃の白金は80mA。
最大公約数40に狙いを定める。
120÷3=40、80÷2=40
0℃の白金3個と125℃の白金2個で電流量が等しくなる。
(6)50mA

0℃白金24個=350℃白金10個
表1より、0℃1個で120mAの電流量。
個数と電流量は反比例なので、
0℃24個の電流量は、120mA÷24個=5mA
350℃白金10個の電流量も5mA。
350℃白金1個の電流量は、5×10=50mA
(7)250mA
同じ個数にしたとき、0℃の白金よりも電流量が半分となる温度を求める。
個数と電流量は反比例なので、〔電流量の半分〕を改めると〔個数が2倍〕
『同じ電流量にしたとき、0℃の白金の2倍の個数となる温度はいくつか』
表3の左側は白金10個単位なので、右側の0℃白金が20個となるところが答え。

表3から左右の関係性を探る。
温度の上昇度合いと0℃白金の個数の増加具合を比べると、
【温度25度の上昇で、0℃白金が+1個増える】
(試しに50℃→350℃で計算すると、300℃の上昇で0℃白金は12個増えている。300÷25=12個)
0℃白金を12個から20個にするので、+8個。
50+25×8=250℃
(8)液体が凝固してしまうから。
*気温を測る気温計に入っている赤い液体は水銀。
水銀は1気圧下の常温で液体を維持する金属。
あれを-200℃の世界に入れたら固まるのではないか?と想像する。
問題文の通り、温度計は『温度とともに規則的に変化する物質の性質』を利用するので、
凝固点以下で液体が固体に凝固してしまうと変化がなくなり、温度が計測できない。
(9)-150℃
今までのおさらい。
白金抵抗温度計は白金に流れる電流量で温度を計測する。
白金に300mA流れた場合の温度はいくらか?

表1で300mAのときの温度が知りたい。
電気をかなり通すので、解答は0℃未満となるはず。
しかし、左右の見比べても温度と電流量の関係性が見出せない。
そこで表3に戻る。
わざわざ白金10個単位で0℃白金の個数との関係を出してきたのは、
〔25℃の上昇で0℃白金の個数が1つ増える〕から。
この関係性を媒介にして考える。
表3より、50℃白金10個では、0℃白金は12個であった。
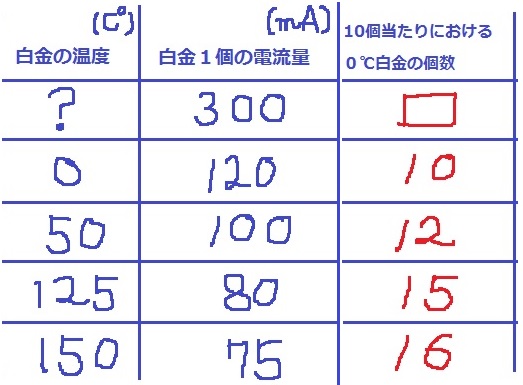
表1の他の温度で、0℃白金の個数を計算すると、125℃が15個、150℃が16個。
0℃は同じ温度なので10個。
白金1個の電流量と、10個当たりにおける0℃白金の個数との関係に注目しよう。
積が1200で一定の反比例。
□=1200÷300=4個
直列に10個つなげると、0℃白金4個を直列したときと同じ電流量になる温度。
〔0℃:10個〕から〔?℃:4個〕と6個減るので、6×25=150℃
0℃から150℃低い、-150℃となる。


コメント