2019年度　新潟県公立高校過去問【数学】解説

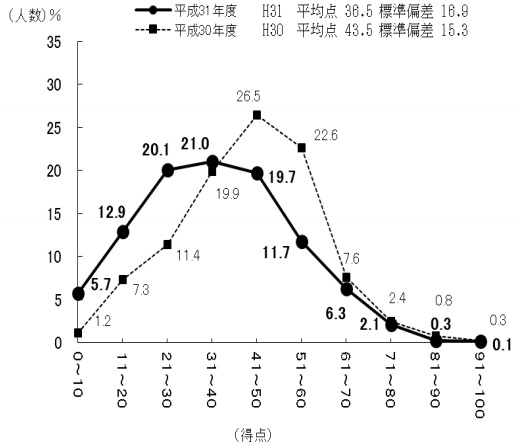
平均36.5点

説明問題が多いです。以下、解答に説明が求められる設問に★をつけています。
問題はコチラ→ＰＤＦファイル

大問１（小問集合）－65.8％

（１）　95.6％
４－９×２
＝４－18＝－14

（２）　89.2％
２（ａ＋２ｂ）－（３ａ－４ｂ）
＝２ａ＋４ｂ－３ａ＋４ｂ
＝－ａ＋８ｂ

（３）　68.5％
ａ⁶ｂ⁵÷ａ²×ｂ³
＝ａ⁴ｂ⁸

（４）　90.5％
連立。ｘ＝２、ｙ＝－１

（５）　89.4％
√45＋√10÷√２
＝３√５＋√５
＝４√５

（６）　56.1％
ｘ²＋７ｘ＝０
ｘ（ｘ＋７）＝０
ｘ＝－７、０

（７）　41.4％
ｘ＝１のとき、ｙ＝ａ
ｘ＝５のとき、ｙ＝25ａ
（25ａ－ａ）/（５－１）＝６ａ＝－12
ａ＝－２
*誤答ではａ＝２が見られた。

（８）　54.4％
底面の半径は５：12：13（三平方）から５ｃｍ。
５×５×π×12×１/３＝100πｃｍ³

（９）　35.1％

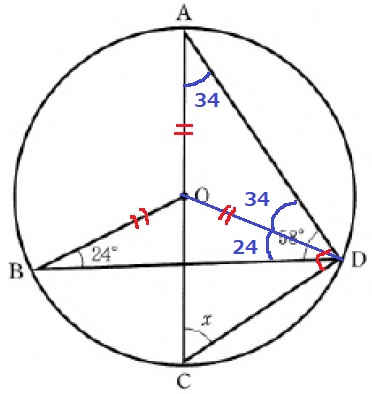
ＯＤに補助線。
半径より、△ＯＢＤは二等辺。
∠ＯＤＢ＝24°
∠ＯＤＡ＝58－24＝34°
△ＯＡＤも二等辺なので、∠ＯＡＤ＝34°
直径ＡＣに対する円周角ＡＤＣは90°
△ＡＣＤで、∠ｘ＝180－（34＋90）＝56°
*誤答では∠ＡＤＢと同じ58°が見られた。

（10）　38.3％
総和･･･【階級値×度数の合計】
階級値は各階級の真ん中の数。
（42×３＋46×４＋50×６＋54×９＋58×５＋62×２＋66×１）÷30
＝1576÷30＝52.53…→52.5ｃｍ

大問２（小問集合２）－32.7％

（１）★　23.4％！
２つの文から１つずつ立式。
ｘ－３＝２（ｙ＋３）…①
ｘ＋２＝ｙ－２＋25…②
代入法で解くと、
ｘ＝２ｙ＋９…①’
ｘ＝ｙ＋21…②’
２ｙ＋９＝ｙ＋21
ｙ＝12
ｘ＝２×12＋９＝33
ｘ＝33、ｙ＝12

（２）★　25.6％！
５枚から３枚のカードを取り出す。
順番は考慮しないので組み合わせ⇒₅Ｃ₃＝10通り
９以下になる組み合わせを調べる。
（１、２、３）（１、２、４）（１、２、５）
（１、３、４）（１、３、５）（２、３、４）
計６通り。
６/10＝３/５
*【全体－10以上の組み合わせ】でもＯＫ！
「以下」の意味を取り違えたミスがあったそうだ。

（３）①　64.4％
距離は４ｋｍ。Ａさんの速さは毎分ｙｋｍ。時間はｘ分。
単位換算の必要はない。速さと時間は反比例。
ｙ＝４/ｘ

②★　6.5％!!
月曜日の時間を【100】とおくと、火曜日の時間は【80】。
時間の比は、100：80＝５：４
速さの比は時間の比の逆比。
月：火＝４：５
５/４倍＝1.25倍
百分率でいえば、25％増加した。

（４）　46.3％
孤ＡＢを１：３に内分する点Ｐを作図する。
孤の長さは中心角の大きさに比例する。
孤を４分の１にするには、中心角を４分の１すればいい。
∠ＢＯＡの二等分線→二等分された角をさらに二等分する。
その線と孤ＡＢとの交点がＰとなる。

大問３（図形の証明）－28.3％

★　28.3％！
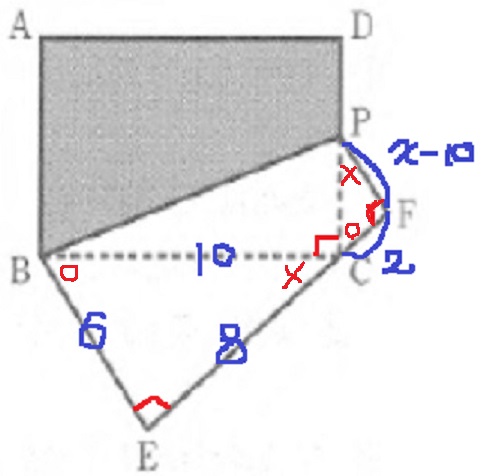
△ＡＢＦ≡△ＢＣＥの証明。

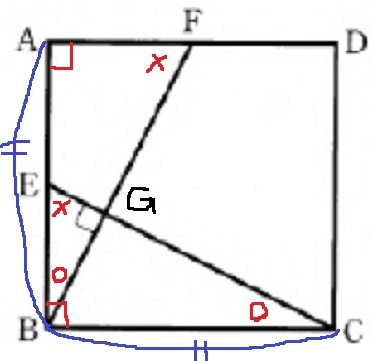
∠ＦＡＢ＝∠ＥＢＣ（正方形の内角）
ＡＢ＝ＢＣ（正方形の一辺）

∠ＥＣＢ＝○、∠ＣＥＢ＝×する。
○＋×＝90°で角度を調査。
△ＥＢＧ内で、∠ＥＢＧ＝○
∠ＥＣＢ＝∠ＦＢＡ（∠ＥＢＧ）
一辺両端角で合同。

大問４（数量変化）－11.8％

（１）　26.3％！
ｘ＝４のとき、ＰはＡＤ上にいる（ｙは三角形）。
ＡＢ（縦）：ＡＤ（横）＝６：10＝３：５
ＡＱ＝４×６/10＝12/５ｃｍ
ｙ＝４×12/５÷２＝24/５

（２）　26.0％！
10＜ｘ≦16→ＰはＤＣ上にいる。
ＡＤ＝10ｃｍで、ｘはＰが動いた距離の合計だから、
ＤＰ＝ｘ－10ｃｍ

（３）①　12.7％！
０＜ｘ≦10（ＰがＡＤ上）
横ＡＰ＝ｘ。
縦ＡＱは10：６の比から、ｘ×６/10＝３/５ｘ
ｙ＝ｘ×３/５ｘ÷２＝３/10ｘ²

②　13.0％！
10＜ｘ≦16（ＰがＤＣ上）

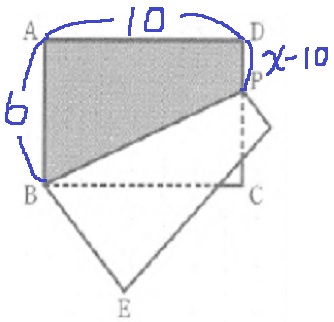
上底ＤＰ＝ｘ－10、下底ＡＱ＝６、高さＡＤ＝10
ｙ＝（ｘ－10＋６）×10÷２＝５ｘ－20

（４）★　1.2％!!
ＣがＥＦに接する。
Ｃがポイントとなるので、Ｃを１つの頂点とする△ＢＥＣに着目。

ＢＥ＝６、ＢＣ＝10
△ＢＥＣで三平方→ＥＣ＝８

ＣＦ＝10－８＝２
折り返しから、ＰＦ＝ＰＤ＝ｘ－10

○＋×＝90°で角度を調査していくと、
２角相等で△ＢＥＣ∽△ＣＦＰ。
ＣＦ：ＦＰ＝ＢＥ：ＥＣ
２：ｘ－10＝６：８
６（ｘ－10）＝２×８
ｘ＝38/３
前問より、ｙ＝５ｘ－20＝130/３
*主な誤答例は、ｘ＝13、ｙ＝45

大問５（規則）－23.2％

（１）
◆ｎ＝７のとき　61.7％
図１で見えているので、そのまま足す。
Ｘ＝２＋12＋６＋８＝28

◆ｎ＝15のとき　38.1％
ｂ（15の下）：15＋５＝20
ｄ（15の右）：３行目の１列目である11。
Ｘ＝10＋20＋14＋11＝55

◆ｎ＝76のとき　24.8％！
76→５の倍数＋１
５の倍数＋１は１列目にあたる。
ａ：76－５＝71
ｂ：76＋５＝81
ｃ：76のある行の５列目→76＋４＝80
ｄ：77
Ｘ＝71＋81＋80＋77＝309

（２）①　39.5％
ｎが２～４列目にある場合。
ａ＋ｂ＝（ｎ－５）＋（ｎ＋５）＝２ｎ
ｃ＋ｄ＝（ｎ－１）＋（ｎ＋１）＝２ｎ
Ｘ＝２ｎ×２＝４ｎ
*誤答例…５ｎ

②　19.6％！
ａ＋ｂ＝２ｎ
ｃ＋ｄ＝（ｎ＋４）＋（ｎ＋１）＝２ｎ＋５
Ｘ＝２ｎ＋２ｎ＋５＝４ｎ＋５

（３）★　0.6％!!!
５列目にｎがあるとき、Ｘ＝４ｎ－５

１列目にｎがある：Ｘ＝４ｎ＋５
２～４列目にｎがある：Ｘ＝４ｎ
５列目にｎがある：Ｘ＝４ｎ－５

Ｘが６の倍数→Ｘは偶数。
４ｎは偶数なので、４ｎ＋５、４ｎ－５は偶数－奇数＝奇数となり、偶数にならない。
したがって、Ｘが６の倍数になるときは、ｎは２～４列目にあると気づく必要がある。

６の倍数は２の倍数（偶数）×３の倍数。
４ｎでは、４が偶数なので、ｎが３の倍数となれば４ｎ（Ｘ）の値が６の倍数になる。
６≦ｎ≦195の範囲で３の倍数の個数を数える。
195÷３＝65
５÷３＝１…２
65－１＝64個…３の倍数の個数

３の倍数でも、５の倍数は５列目、５の倍数＋１は１列目にくるので、これらを除外する。
（以下、６≦ｎ≦195）
◆５列目
３と５の最小公倍数15の倍数⇒15、30、45…
195÷15＝13個

◆１列目
３の倍数かつ５で割ると余り１⇒６、21、36…
６からはじまり、15ずつ増えていく。
15で割って余りが６になる数（逆にいえば、６引いて15で割り切れる数）。
先ほど、195は15で割り切れたので、195＋６＝201
その１個前の201－15＝186が最後の数。
（186－６）÷15＋１＝13個（＋１で最初の６を数える）
64－13－13＝48個

*はじめに偶数・奇数の判定で２～４列目のＸ＝４ｎに的を絞る。
６の倍数の性質から、ｎが３の倍数であればいい。
しかし、１列目と５列目に登場する３の倍数を除外する。
公式解答では、『そのうち、５で割った余りが０と１である自然数の26個は適さないので』
…とサラっと書かれてあるが、26を出すのが一苦労である・・。

大問６（空間図形）－26.3％

（１）　72.6％・58.4％
ＥＧ…△ＥＨＧで三平方。10ｃｍ
ＥＣ…△ＣＥＧで三平方。10√２ｃｍ

（２）★　33.8％

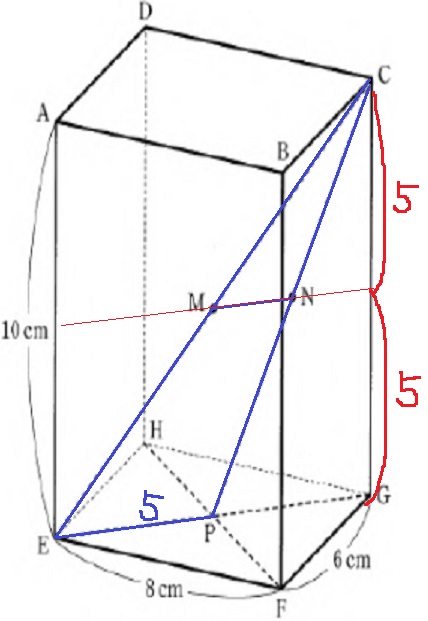
ＭとＮはそれぞれの中点なので、
中点連結定理より、ＭＮ＝５÷２＝５/２ｃｍ

（３）★　13.9％！
上の図を参照。
△ＥＭＮで、底辺５/２ｃｍ、高さ５ｃｍの三角形。
５/２×５÷２＝25/４ｃｍ²

（４）★　0.4％!!!
前問で△ＥＭＮの面積を出したので、
これを底辺とする高さがわかればいい。

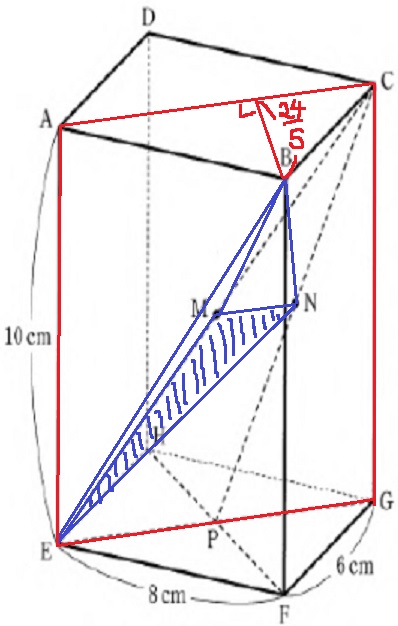
三角錐Ｂ－ＥＭＮが見づらいアングルである…(；^ω^)
△ＥＭＮは面ＡＥＧＣ上にある。
三角錐Ｂ－ＥＭＮの高さは、ＡＣとＢの距離に等しい。
ＡＣとＢの距離は△ＡＢＣの面積24ｃｍ²、底辺ＡＣ10ｃｍから、
24×２÷10＝24/５ｃｍ
25/4（底辺△ＥＭＮ）×24/５（高さ）×１/３＝10ｃｍ³
*主な誤答例…高さを５ｃｍとして計算。
公立高校入試解説ページに戻る