問題PDF
以下の問いに答えなさい。
数値が割りきれない場合は小数第2位を四捨五入して、小数第1位まで答えなさい。
問1

長さが84cmの太さが一定でないバットを糸を使ってつるし、水平にすることを考えます。図1のようにするには540gの力が、図2のようにするには180gの力が必要でした。図3のように、糸1本だけでバットをつるすにはバットの左端から何cmのところをつるせばよいですか。また、このとき糸を支える重さは何gですか。
ものをその一点支えることができるとき、その点を「重心」といいます。例えば、図3で糸を支えている位置(ばねばかりの位置)はバットの重心の真上になります。
一見複雑で重心の位置がわからないように見えるものも、様々な方法で調べることができます。その方法の1つに、「そのものを適当な部分に分け、その部分ごとの重心を考えることで、全体の重心を求める」というものがあります。重さが無視できるほど軽く、曲がらない真っ直ぐな棒をつかい、この方法で、いろいろなものの重心の位置を考えてみましょう。
問2
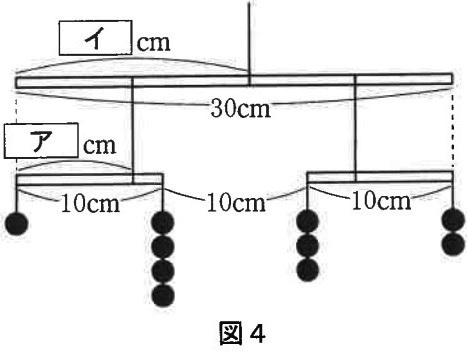
重さ10gのおもり10個を図4のように10cmの棒2本に取り付け、
それを棒の外側の端が揃うように30cmの棒につり下げます。
すべての棒が水平に保たれているとき、図中のア・イの長さはそれぞれ何cmでしょうか。

実は図5のように10gのおもり10個を30cmの棒に取り付けたとき、棒に糸をつけて水平に保てる〔 ウ 〕の長さは〔 イ 〕の長さに等しくなります。このように、一見複雑で重心の位置がわかりにくいものも、うまく分けてその部分ごとに重心を求めることで、全体の重心を求めることができます。

厚さが一定の変形しない板(横80cm×縦50cm)から図6のような形を切り取りました。図7は切り取られて残った部分を表しています。なお、板の大きさがわかりやすいように、縦横10cmごとに破線が描かれています。また、板をつるしている糸はすべて同じ長さであるとします。
問3

切り取った板を図8のように60cmの棒に、両端の位置が揃うように取り付けました。このとき、棒が水平に保たれるためには図中の〔 エ 〕の長さをいくらにすればよいでしょうか。なお、板を図9のように10cmごとに切って棒に取り付けても、棒を水平に保つために支える位置は同じになります。
問4
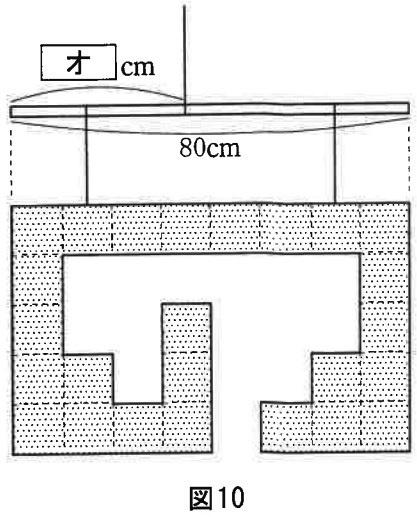
切り取られて残った部分を図10のように80cmの棒に、両端の位置がそろうように取り付けました。このとき、棒が水平に保たれるためには、図中の〔 オ 〕の長さをいくらにすればよいでしょうか。なお、切り取られる前の板の重心は、板の中心になります。
問5
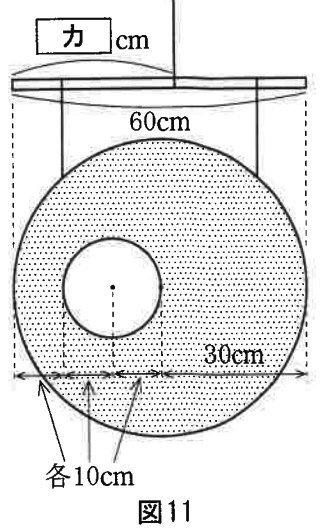
図11のように厚さが一定の半径30cmの円形の板から半径10cmの円形の板が切り取られて残った部分があります。この板を図のように60cmの棒に、2つの円の中心を結んだ線と棒が平行になるように、板が棒の幅にちょうどおさまるように取り付けました。このとき、棒が水平に保たれるためには、図中の〔 カ 〕の長さをいくらにすればよいでしょうか。
@解説@
問1:左端から…21cm、重さ…720g

支点△をこのように設置する。
左側のばねばかりが重いということは、左側が支点との距離が近い。
重さの比が540:180=③:①
支点からの距離は逆比で①:③
支点は左から、84×①/④=21cm
糸を支える重さ=バットの重さは、540+180=720g
問2:ア…8cm、イ…16cm
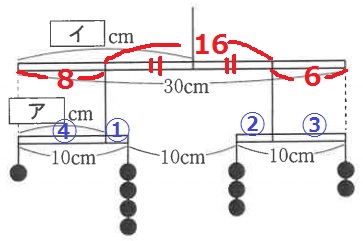
モーメントの計算。【重さ×支点からの距離】が等しいと釣り合う。
ア:10×4/5=8cm
10cmの棒は30cmの棒の左端から8cm、右端から6cmの場所にぶら下がっている。
あいだの長さは、30-(8+6)=16cm
どちらも重り5個分と10cmの棒で重さの合計が等しい。
支点は両者の中点にある。
イ:8+16÷2=16cm
問3:31cm
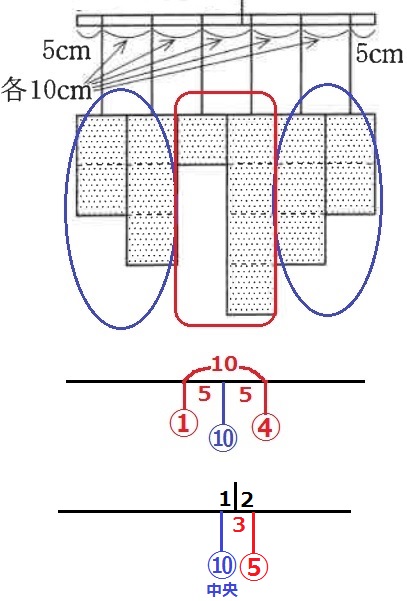
両サイドの青が左右対称なので、中央に⑩を集める。
①と④は距離が10cm。4:1に内分して④の左2cmに⑤を集める。
最後に⑩と⑤のあいだの3cmを1:2に内分。
支点は左から、30÷2+1=16cm
問4:39.4cm
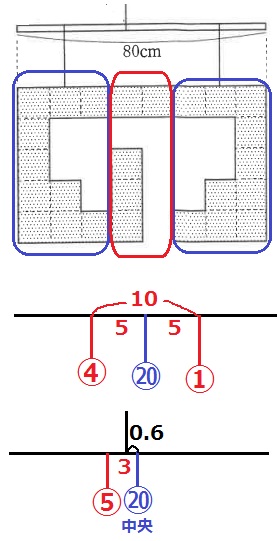
左右の3列が左右対称。中央に⑳を集める。
④と①のあいだの10cmを1:4に内分。④から右2cmに⑤。
⑤と⑳のあいだの3cmを4:1に内分。
支点は⑳から3×1/5=0.6cm左にある。
80÷2-0.6=39.4cm
問5:31.25cm
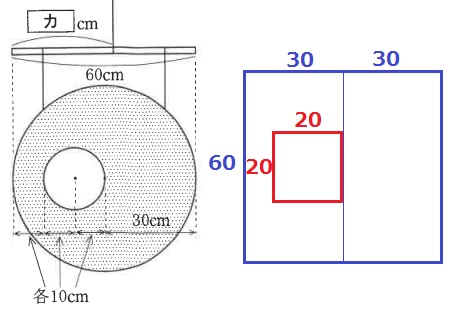
円を正方形に置き換えてみる。
切り取られた小さな正方形と全体の大きな正方形は相似形なので問題なし。
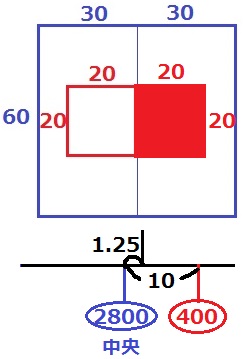
左右対称戦法。
20×20の正方形を右側につくる。
2つの正方形以外の面積を重さとみなして計算する。
60×60-20×20×2=2800
周りの合計が2800で、これを中央に集める。
赤い正方形400の重心は中央から右10cmのところ。
2800:400=7:1
全体の重心は2800から、10×1/8=1.25cm右側にある。
左から60÷2+1.25=31.25cm


コメント