2020年度　山梨県公立高校入試問題過去問【数学】解説

平均53.9点（前年比；－1.7点、最高97点、最低０点）

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）　97％
10－（－４）
＝10＋４＝14

（２）　84％
７/15×（－３）＋４/５
＝－７/５＋４/５
＝－３/５

（３）　98％
（－３）²＋７
＝９＋７＝16

（４）　95％
√24＋８√６
＝２√６＋８√６
＝10√６

（５）　89％
27ｘｙ×ｘ²÷（－９ｘ²ｙ）
＝－３ｘ

（６）　87％
３（ｘ＋６ｙ）－２（ｘ＋８ｙ）
＝３ｘ＋18ｙ－２ｘ－16ｙ
＝ｘ＋２ｙ

大問２（小問集合）

（１）　75％
２ｘ²－７ｘ＋４＝０
因数分解ができないので解の公式。
ｘ＝（７±√17）/４

（２）　47％
『ＡＢ、ＡＣまでの距離が等しい点』
→∠ＢＡＣの二等分線
これとＢＣとの交点に●をかく。

（３）　79％
比例；ｙ＝ａｘ
（ｘ、ｙ）＝（－３、36）を代入。
36＝－３ａ
ａ＝－12
ｙ＝－12ｘ

（４）　41％
４本中３本が当たりだから、Ａが当たる確率は３/４
Ａがひいたくじは戻すので、Ｂが当たる確率は３/４で同じ。
２人とも当たる確率は、３/４×３/４＝９/16

（５）①　86％

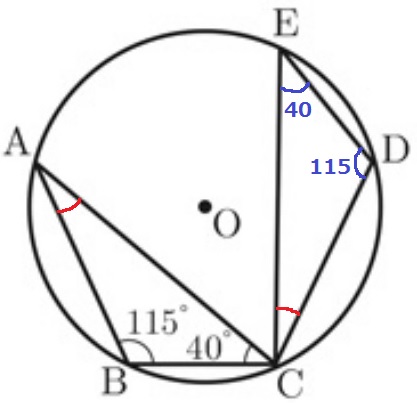
対応する角に気をつけよう。
∠ＥＣＤ＝∠ＣＡＢ＝180－（115＋40）＝25°

②　45％

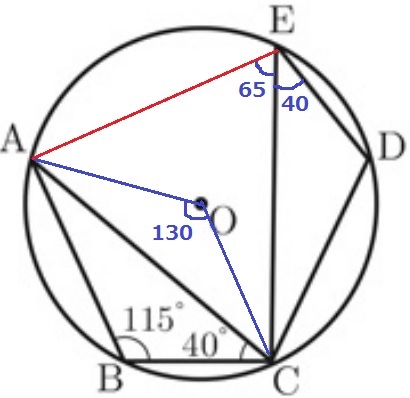
ここで130°を用いる。
Ａの回転先はＣ。∠ＡＯＣ＝130°
この円周角である∠ＡＥＣ＝130÷２＝65°
∠ＣＥＤ＝∠ＡＣＢ＝40°なので、∠ＡＥＤ＝65＋40＝105°
イ

大問３（データの活用）

（１）①　88％
最頻値（モード）…最もあらわれている値。
2.0ｇ

②　61％
424個の中央値（メジアン）は212番目と213番目の平均→2.2ｇ
ウ

（２）①記号―88％、説明―58％（部分正答11％）
イ；キャップと回収箱の合計の重さから空の回収箱の重さを引き、
その差をキャップ１個あたりの重さで割る。
*キャップの個数を求める方法を説明する。
（合計の重さ－回収箱の重さ）÷キャップ１個の重さ＝キャップの個数

②　14％！
標本調査。
無作為に取り出した50個のうち、印付きは４個。
印付きは全部で100個だから、50×100/４＝1250個

大問４（整数）

（１）　43％
ａやｂの中身は考えない。問題文から等式を立てる。
ａ－ｂ＝－18
ｂ＝ａ＋18

（２）　37％
18の倍数にならない反例を挙げる。
ａとｂの差が18未満だと18の倍数にならない。
12と21の差は９で×。（ア：21、イ：９）
34と43もダメ。（ア：43、イ：９）
ｘとｙの値が１違いだと差が９になるからである。

後ろの設問でやるが、ｘ－ｙが奇数だとダメ。
ａが10、30、50もダメ。14、18、27、38どれも差が奇数でダメ。
位の数の差が奇数ということは、ａが奇数であればｂは偶数となり、
ａが偶数であればｂは奇数となる。（27は奇数だが72は偶数のように）
奇数－偶数も偶数－奇数も奇数だから、ａとｂの差が偶数の18の倍数にはならない。

（３）①　27％！
情報整理が問われる。
問題文より、ａ－ｂ＝９（ｘ－ｙ）
この値が54であり、ｘ＝８を代入してｙを求める。
９（８－ｙ）＝54
ｙ＝２
（ｘ、ｙ）＝（８、２）
ｘはａの十の位、ｙはａの一の位なので、ａ＝82
ｂはそれを逆にした数だから、ｂ＝28

②条件―14％！（部分正答１％）、最大値―13％！
９（ｘ－ｙ）のｘ－ｙが整数だから、９（ｘ－ｙ）は９の倍数。
さらに、９（ｘ－ｙ）が18の倍数といえるには、ｘ－ｙが２の倍数（偶数）のとき。
（９の倍数×２の倍数＝18の倍数）
ｘとｙは位の数なので０≦<x,ｙ≦９
偶数の最大値は８（９－１＝８、８－０＝８）
（ｘｰｙが）２の倍数である、最大値：ｘ－ｙ＝８

大問５（関数）

（１）　78％
ｙ＝ａｘ²にＡ（－２、２）を代入。
２＝（－２）²ａ
ａ＝１/２

（２）　17％！

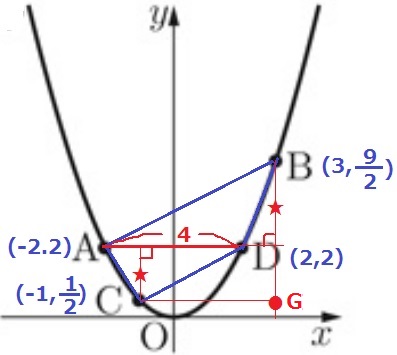
４つの座標を確認。ＡとＤのｙ座標は等しい。
四角形ＡＣＤＢをＡＤで分割して△ＡＢDと△ＡＣＤに分ける。
ＡＤ＝４
２つの三角形の高さは★のところ。その合計はＢＧにあたる。
ＢＧ＝９/２－１/２＝４
四角形ＡＣＤＢの面積は、４×４÷２＝８

（３）①　38％
ＥとＦの座標を確認。
Ｅ（－３、９/２）
Ｆ（４、８）
Ｅ→Ｆは右に７、上に８－９/２＝７/２移動する。
傾き（変化の割合）はｙの増加量÷ｘの増加量→７/２÷７＝１/２
Ｆから左に４移動すると、傾きは１/２だから下に２移動する。
切片は８－２＝６
ｙ＝１/２ｘ＋６

②　２％!!

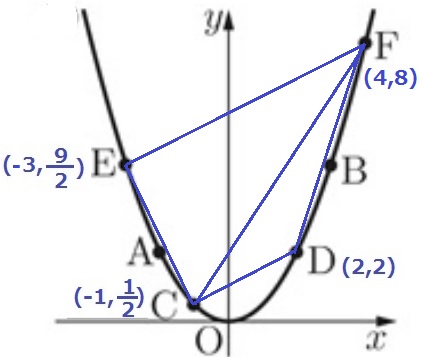
なんとなくＥＦとＣＤが平行にみえる。
試しにＣＤの傾きを調べてみる。
Ｃ→Ｄは右に３、上に２－１/２＝３/２
傾き（変化の割合）は、３÷３/２＝１/２
前問でＥＦの傾きは１/２だったから、やはりＥＦ//ＣＤ

四角形ＡＥＣＤは１組の対辺が平行な台形となる。
台形を対角線で分割した２つの三角形の面積比は上底：下底の比。
すなわち、△ＦＥＣ：△ＦＣＤの面積比はＥＦ：ＣＤに相当する。

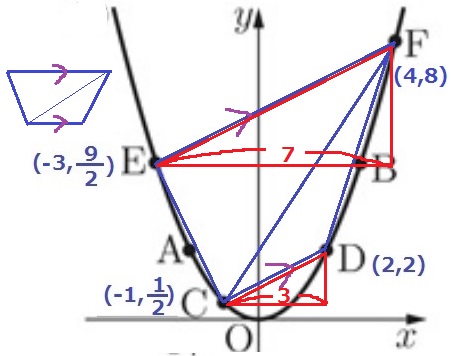
ＥＦとＣＤを斜辺とする、２つの直角三角形は相似。
各々の辺の比はｘ座標の差から７：３。
ＥＦ：ＣＤ＝７：３
△ＦＥＣ：△ＦＣＤの面積比は７：３。

大問６（平面図形）

（１）　24％！（部分正答55％）
△ＡＢＨ∽△ＡＯＤの証明。

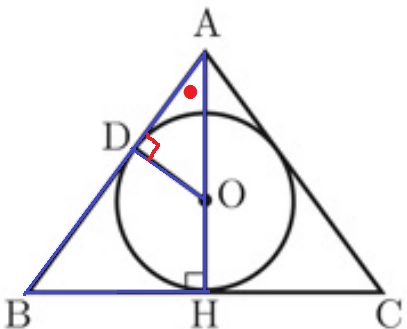
共通角●。
接点Ｄから接線ＡＢと半径ＯＤは直交する→∠ＯＤＡ＝90°
２角相等で∽。

（２）①　81％
△ＡＢＨで三平方。
ＡＨ＝√（６^２－４²）＝２√５ｃｍ

②　６％!!
円Ｏの面積を求めるには、半径ＯＤが知りたい。
ＯＤは△ＡＯＤの１辺。
そこで、（１）の△ＡＢＨ∽△ＡＯＤを用いる。
ＡＨ：ＢＨ＝ＡＤ：ＯＤ
ＡＤの長さが不明。

ＢＯに補助線。
共通辺ＯＢ、半径ＯＤ＝ＯＨ、垂直
→斜辺と他の１辺が等しい直角三角形で△ＢＯＤ≡△ＢＯＨ
（内接円の問題によくでてくる）
ＢＤ＝ＢＨ＝４ｃｍ
ＡＤ＝６－４＝２ｃｍ

ＡＨ：ＢＨ＝ＡＤ：ＯＤ
２√５：４＝２：ＯＤ
ＯＤ＝４×２/２√５＝４√５/５
円Ｏの面積は、（４√５/５）²π＝16/５πｃｍ²

（３）①　４％!!
△ＡＢＣは１辺６ｃｍの正三角形。

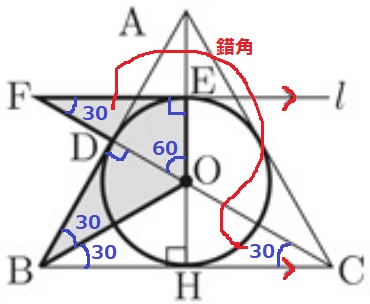
△ＢＯＤ≡△ＢＯＨから∠ＯＢＤ＝30°（内接円の中心（内心Ｏ）は∠ＡＢＣの二等分線にある）
同様に∠ＯＣＢ＝30°、直線ℓ//ＢＣより、錯角で∠ＯＦＥ＝30°
接線と半径は垂直に交わるので、∠ＯＤＢ＝ＯＥＦ＝90°
△ＯＤＢと△ＯＥＦの内角はともに30°－60°－90°で、
半径ＯＤ＝ＯＥを加味すると、１辺と両端角が等しく合同。

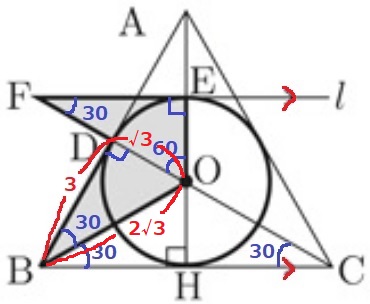
ＣＤは△ＡＢＣを２等分する→ＢＤ＝３ｃｍ
△ＯＤＢの辺の比は１：２：√３だから、
ＤＯ＝√３ｃｍ、ＢＯ＝２√３ｃｍ

〔図形Ｔの周の長さ＝△ＯＤＢ＋△ＯＥＦ－ＯＤ×２〕
△ＯＤＢの周の長さを２倍して、重複するＤＯを２倍した長さを引く。
（３＋√３＋２√３）×２－√３×２
＝４√３＋６ｃｍ

②　１％!!!

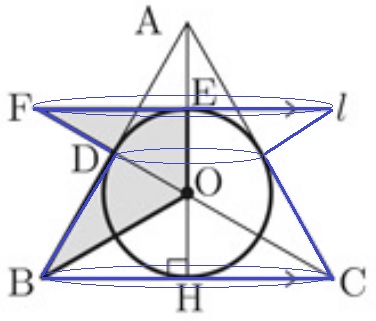
↑こんな感じの立体の体積を求めます(´ﾟдﾟ｀)
どういう切り口で挑めばよいのやら・・。

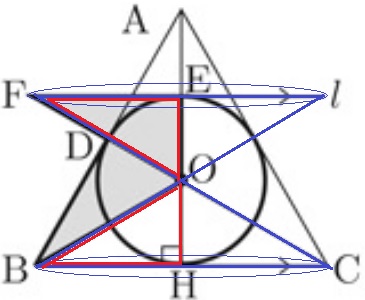
△ＯＥＦと△ＯＨＢは合同なので、
回転させたときの円錐の体積も同じである。

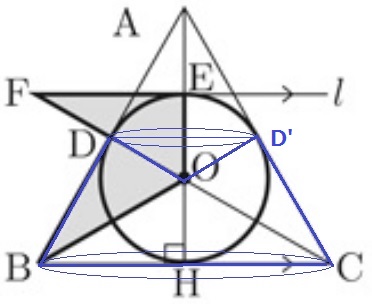
△ＯＥＦを△ＯＨＢに引越しさせて回転させる。
正面からみると台形ＤＢＣＤ’の回転体（円錐台）から、
二等辺三角形ＤＯＤ’の回転体（円錐）を引くイメージ。

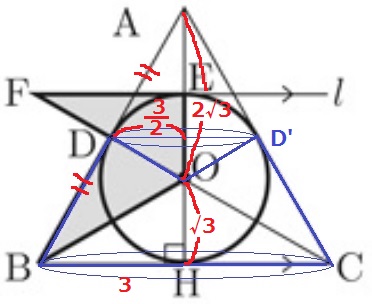
辺の比が１：２：√３の直角三角形より、ＡＯ＝２√３ｃｍ、ＯＨ＝√３ｃｍ
ＤはＡＢの中点なので、Ｄから回転の軸までの距離は３÷２＝３/２ｃｍ

体積の算出は底辺の半径３ｃｍ、高さ３√３ｃｍの円錐から、
上部にある底辺の半径３/２ｃｍ、高さの合計２√３ｃｍの円錐を引くと計算しやすい。
３×３×π×３√３÷３－３/２×３/２×π×２√３÷３
＝９√３π－３√３/２π
＝15√３/２πｃｍ³