2021年度　灘中学過去問【理科】大問６解説

問題ＰＤＦ
〔Ａ〕ある日、太郎くんは知り合いの金属加工業の人から金属製のコーン（円錐形）をもらいました。コーンは側面だけがあり、中身と底面はありません。好きなように加工してあげるよ、と言われたので実験してみました。面の厚みは一定とします。

問１
図１のようにコーンの中心軸ＡＢのちょうど真ん中の点Ｃのところに糸をつけてつり下げるとどうなるでしょうか。正しいものを選びなさい。

ア：Ａが下がる。　イ：Ｂが下がる。

問２
次に、コーンの真ん中よりもＢに近い点Ｄのところに糸をつけてつり下げると、ＡＢが水平になってつりあいました。点Ｄの位置を測ってみると長さの比はＡＤ：ＤＢ＝２：１になっていました。糸をはずし、コーンのＤのところで（ＡＢに垂直な平面で）切断してもらってＡ側とＢ側の２個に分けました。
（１）それらの重さのはかるとどうなっているでしょうか。正しいものを選びなさい。
ア：Ａ側のほうが重い。　イ：Ｂ側のほうが重い。　ウ：重さは等しい。

（２）Ａ側の重さとＢ側の重さの比を、整数比で答えなさい。

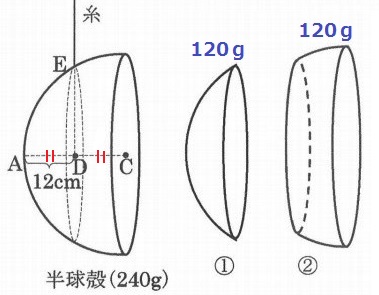
〔Ｂ〕またある日、太郎くんはその人から、図２のような直径48ｃｍ重さ480ｇの金属製の球殻（中がからっぽの球のこと）をもらいました。好きなように加工してあげるよ、と言われたので、球の中心Ｃを通る平面で切断して（Ａ側とＢ側の）２個の半球殻に分けてもらって、実験をしてみました。面の厚みは一定とします。
図３のように、Ａ側の半球殻に糸をつけてつり下げてみたところ、「中心軸ＡＣ上でＡから12ｃｍの点Ｄにおける、ＡＣに垂直な直線」が球面と交わる点Ｅに糸をつけたとき、中心軸ＡＣがちょうど水平になってつり合うことを太郎くんは発見しました。糸をはずして、点Ｄを通りＡＣに垂直な平面で半球殻を切断してもらい、図４の①と②の２個に分けて、それぞれの重さをはかりました。するとどちらも120ｇだったので、太郎くんはおどろきました。太郎くんは考えて、あることを思いつき、それを確かめるために、その人にたのんで、残ったＢ側の球殻（図５）を３個に切断してもらいました。その３個の重さをはかると、太郎くんの予想通り、どれも80ｇでした。

問３
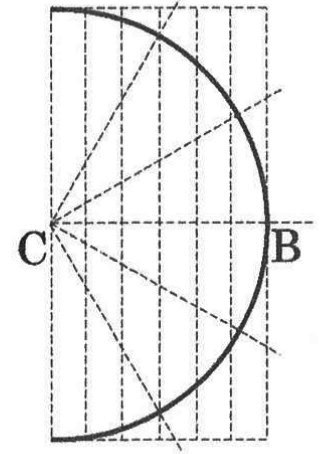
どのように切断してもらったと思いますか。
解答らんの図に、切断面を表す２本の直線をかきなさい。

問４
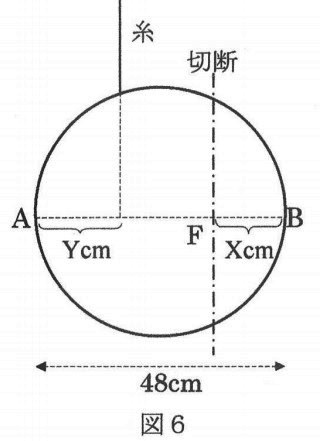
新たに球殻を用意し、図６のように、直径ＡＢのＢからＸｃｍの点Ｆを通り、ＡＢに垂直な平面で球殻を切断し、Ｂ側を捨てます。残ったＡ側に糸をつけて、ＡＦが水平になるようにつり合わせるためには、糸をつける位置を、Ａから何ｃｍのところにすればよいでしょうか（図のＹｃｍをいくらにすればよいか）。Ｙを、Ｘを用いた式で表しなさい（式の書き方はいろいろあるのでどのように書いてもよい）。

問２（１）イ
間違われやすいが、中学受験では既出ゆえ間違えられない。

重りを描くとわかりやすい。
支点から距離の短いＢ側が重い。

（２）Ａ側：Ｂ側＝４：５

理科というより算数。
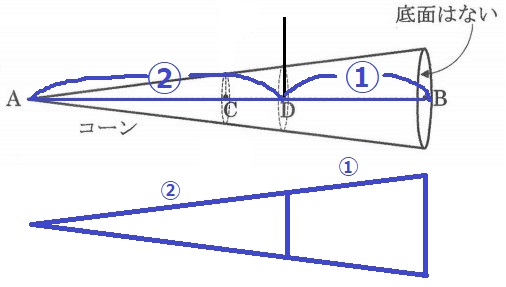
ＡＤ：ＤＢ＝②：①
横から見た図で辺の比を②：①として考える。
コーンの中身はなく、面の厚みが一定の円錐形なので、
面積を重さとみなし、面積比で計算する。
Ａ側…②×②＝【４】
Ｂ側…③×③－【４】＝【５】
Ａ：Ｂ＝４：５

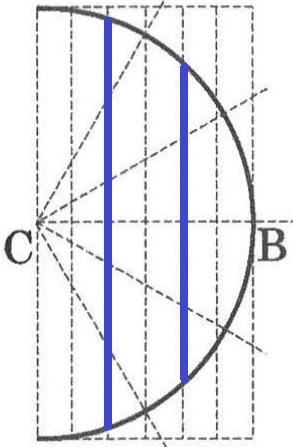
問３：下図参照。

ＡＣの中点を通るＤ－Ｅ面で割ったら、重さがちょうど半分ずつになったという。
なんとなく②の方が重そうだが(;`ω´)
半分になったのは、ＤがＡＣの中点だからではないか？

半球240ｇで３個に分けたら80ｇずつになったということは、
半径ＣＢをそのまま３等分すればよいのでは？

↑これが正解。

問４：Ｙ＝（48－Ｘ）÷２

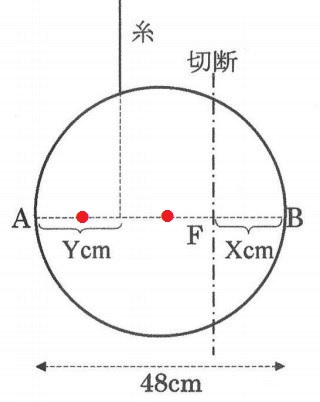
予想さえ立てられたら、すぐ解けてしまう。。
ＡＦの中点の真上に糸を吊るせばいい。

＠＠＠

ところで、、
なぜそうなるのか？？？

サボも知らないので調べてみたら、それっぽいのを見つけました。

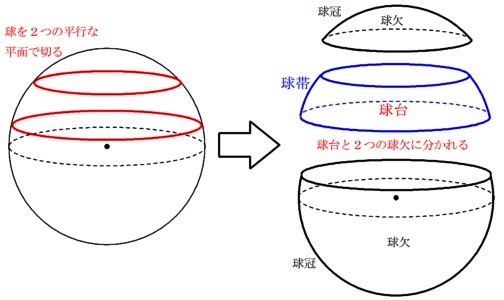
Fukusukeの数学めもより。
球を１つの平面で切ると球欠、その曲面を球冠といい、
球を２つの平面で切ったあいだの部分を球台、その曲面を球帯というそうです。

面積を重さとみなしているので、
円の直径を３等分したら球冠・球帯の面積も３等分されることになります。

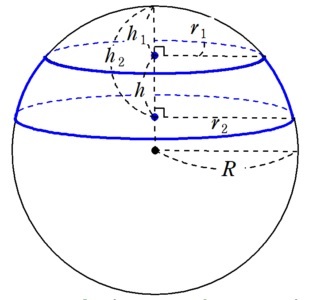
【球帯の面積は、もとの球から切断するときの厚さｈに比例する】
スッキリして美しいですね(‘ω’)

ｒ₂の球冠の面積からｒ₁の球冠の面積を引くことで球帯の面積が求まります。
もとの球の半径をＲとすると、球冠の面積Ｓ＝２πＲｈ

２πＲｈ₂－２πＲｈ₁
＝２πＲ（ｈ₂－ｈ₁）
＝２πＲｈ
πは円周率で定数、球の半径Ｒを固定すれば球帯の面積Ｓの値はｈに依存する。

なぜ球冠の面積は２πＲＨなのか。こちらのページを読んで、自分で考えてみましょう( ‘ᾥ’ )
難関中学（理科）解説ページに戻る