2021年度　豊島岡女子学園中学３回目過去問【算数】大問６解説

問題ＰＤＦ
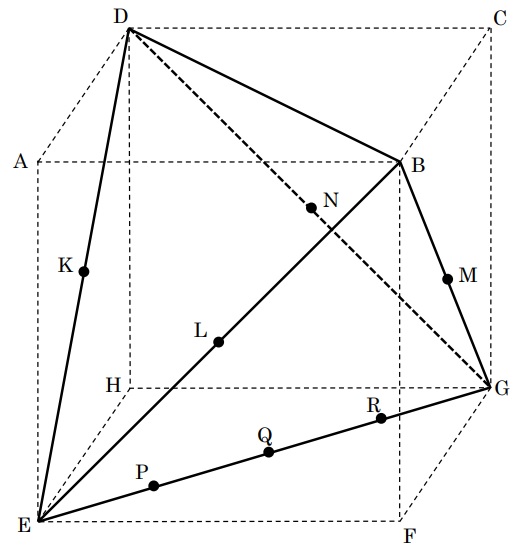
下の図のように、１辺の長さが12ｃｍの立方体ＡＢＣＤ－ＥＦＧＨの頂点Ｂ、Ｄ、Ｅ、Ｇを結んでできる三角すいを立体（あ）とします。立体（あ）の辺ＤＥ、ＢＥ、ＢＧ、ＤＧの真ん中の点をそれぞれＫ、Ｌ、Ｍ、Ｎとし、辺ＥＧを４等分する点をＥに近い方からＰ、Ｑ、Ｒとします。このとき、次の各問いに答えなさい。

（１）
立体（あ）を４つの点Ｋ、Ｌ、Ｍ、Ｎを通る平面で切り分けたとき、
点Ｑを含む立体を（い）とします。立体（い）の体積は何ｃｍ³ですか。

（２）
（１）の立体（い）を３つの点Ｋ、Ｌ、Ｐを通る平面と、
３つの点Ｍ、Ｎ、Ｒを通る平面で切り分けたとき、
点Ｑを含む立体を（う）とします。立体（う）の体積は何ｃｍ³ですか。

（３）
（２）の立体（う）の３つの辺ＫＰ、ＬＰ、ＭＰの真ん中の点をこの順にＸ、Ｙ、Ｚとします。
３つの点Ｘ、Ｙ、Ｚを通る平面で立体（う）を切り分けたとき、
点Ｑを含む立体の体積は何ｃｍ³ですか。

＠解説＠
（１）

中の立体は、立方体からＡ・Ｃ・Ｆ・Ｈを頂点とする４つの三角錐を切り落とした図形。
12×12×12－12×12÷２×12÷３×４
＝12×12×12－12×12×８
＝12×12×（12－８）＝576ｃｍ³

立方体から同じように切り落とすので、切り落とした４つの三角錐はすべて合同。
これらの底面の三角形（△ＢＥＧ・△ＢＤＥ・△ＢＤＧ・△ＤＥＧ）は、
立方体の面（正方形）の対角線を１辺とする正三角形で合同⇒中の立体は正四面体である。

これをＫＬＭＮで切り分けたときの側面に注目。
側面の正三角形を●と■に分けると、上も下も面は●が２つ、■が２つ、四角形ＫＬＭＮで同じ形。
つまり、上と下も同じ立体であり、求めたい立体（あ）は正四面体の半分である。
576÷２＝288ｃｍ³

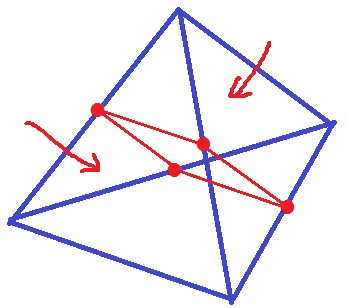
*４辺の中点で切断すると、正四面体は合同に２等分される。

（２）

正四面体Ｄ－ＢＥＧから、三角錐Ｋ－ＬＥＰの体積を隣辺比で算出。
576×１/２×１/２×１/４＝36ｃｍ³
三角錐Ｎ－ＭＧＲについても同様で36ｃｍ³。
立体（い）の体積は、288－36×２＝216ｃｍ³

（３）

これも側面の正三角形から図形の特徴をつかむ。
△ＢＭＬと△ＢＧＥは相似で、ＥＧ＝④とすると相似比でＬＭ＝②
ＰＲ＝④÷２＝②
△ＤＮＫと△ＤＧＥも同様に相似でＫＮ＝②となり、ＬＭ＝ＰＲ＝ＫＮ
同位角も等しいから平行、ＬＭ//ＰＲ//ＫＮ

さらに、正三角形ＢＧＥは左右対称でＬＭとＰＲの長さが同じということは、
ＬＭを真下にスライドするとＰＲとなり、ＬＰとＭＲは底辺ＥＧに垂直に交わる。
（ＢからＥＧに垂線をひき、左右で相似を使ってもよい）
四角形ＬＰＲＭは長方形で、同様に、四角形ＫＬＭＮと四角形ＫＰＲＮも長方形である。
ここから側面の３つが長方形だから、立体（い）は三角柱である。
ＸＹＺが通過する断面は長方形ＫＬＭＮに平行である。

三角柱（い）：三角柱（う）＝△ＫＬＰ：△ＸＹＰ
＝【４】：【１】
立体（う）の体積は、216×１/４＝54ｃｍ³
難関中（算数科）解説ページに戻る