2022年度　灘中学過去問【理科】大問１解説

問題ＰＤＦ
図１のような小さな圧力センサーを使って実験をします。
圧力センサーは、その上にたとえば50ｇのおもりをのせると「50ｇ」と表示される装置です。

　図２のように、正三角形ＡＢＣをかいた軽い板を用意し、各頂点Ａ、Ｂ、Ｃの真下にそれぞれセンサーを並べて、その上に板を乗せます。３個のセンサーを頂点と同じ記号Ａ、Ｂ、Ｃで区別しておきます。板の重さは無視します。
　板の上に何も置かないときはセンサーの表示はＡ、Ｂ、Ｃの順に（０ｇ、０ｇ、０ｇ）です。たとえば頂点Ｂに50ｇのおもりを置いたときは、表示は（０ｇ、50ｇ、０ｇ）です。以下では、単位を省いてＡ、Ｂ、Ｃの順に数字を並べて（０、50、０）のように表すことにします。
　いま、Ｂに50ｇのおもりを置き、辺ＢＣ上でＢからＣまで少しずつ、そのおもりの場所を変えながらセンサーの表示を読み取りました。その結果が図３のグラフです。

問１
次の文の①、②にあてはまる数値を答えなさい。
  
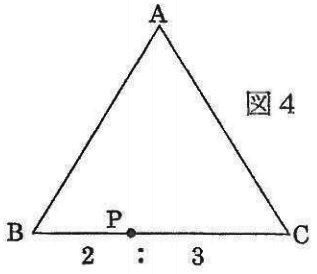
『図４のように、辺ＢＣを２：３に分ける点Ｐに50ｇのおもりを置く。このとき、センサーの表示は（０、①、②）となる。このおもりの置き方は、点Ｂに①ｇのおもりを置き、点Ｃに②ｇのおもりを置いた場合と同等である。つまり１個のおもりを適切な２個のおもりに置きかえることができる』

問２
点Ａに30ｇのおもりを置き、点Ｐに60ｇのおもりを置いた場合、センサーの表示はどうなりますか。（　、　、　）の形で答えなさい。

問３
問２と同じ表示をおもり１個だけを置いて実現するためには、何ｇのおもりをどの場所に置けばよいですか。おもりの重さを答え、場所を図示しなさい。
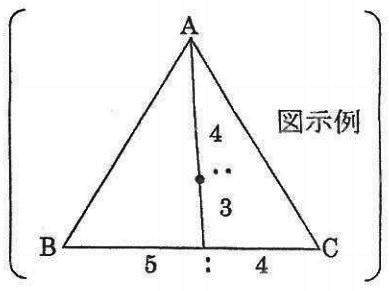
（図示のしかたは図示例にならいなさい。以下同様）
 

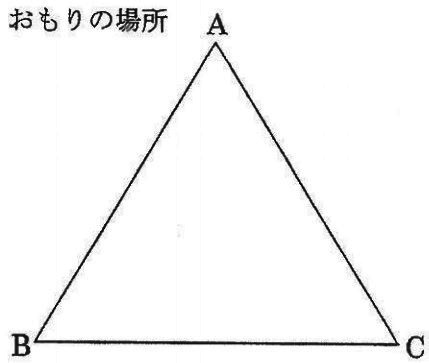
問４
おもり１個だけを置いてセンサーの表示が（50、30、70）になるようにするためには、何ｇのおもりをどの場所に置けばよいですか。おもりの重さを答え、場所を図示しなさい。

問５
辺ＡＢ、ＢＣ、ＣＡのそれぞれのまん中の点を順にＤ、Ｅ、Ｆとします。点Ｄ、Ｅ、Ｆにおもりを１個ずつ置いて、問４の表示を実現するためには、それぞれ何ｇのおもりを置けばよいですか。

ＢＣ上を移動しているとき、
Ａは常に０ｇで、おもりの重さはＢとＣに配分されている。

配分の割合はおなじみの方法。
Ｐを支点にして距離がＢＰ：ＰＣ＝２：３だから、重さは逆比でＢ：Ｃ＝３：２
Ｂ＝50×３/５＝30
Ｃ＝50－30＝20

問２：（30、36、24）
問題文より頂点Ｂに50ｇを置いたら（０、50、０）だったので、
頂点Ａにおいた30ｇは全部Ａにのしかかる。
辺ＢＣ上のＰ60ｇは先ほどと同じ処理をする。
Ｂ＝60×３/５＝36
Ｃ＝60－36＝24
（30、36、24）

問３：おもりの重さ…90ｇ、おもりの場所…下図

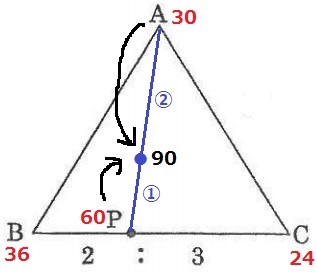
逆の流れをする。
Ｂ36ｇとＣ24ｇを集めてＰ60ｇなので、
Ａ30ｇとＰ60ｇを集めて90ｇ。
場所は重りの比の逆比で60：30＝②：①
ＡＰを２：１に内分する点に90ｇをのせる。

問４：おもりの重さ…150ｇ、おもりの場所…下図

Ｂ30ｇとＣ70ｇを集めて100ｇ。距離は⑦：③。
Ａ50ｇと100ｇを集めて150ｇ。距離は△２：△１。

問５：Ｄ…10ｇ、Ｅ…50ｇ、Ｆ…90ｇ
ここで差が開くか。

Ｂに置いた50ｇがＢＣの中点にきたとき、ＢとＣではそれぞれ25ｇが表示された。

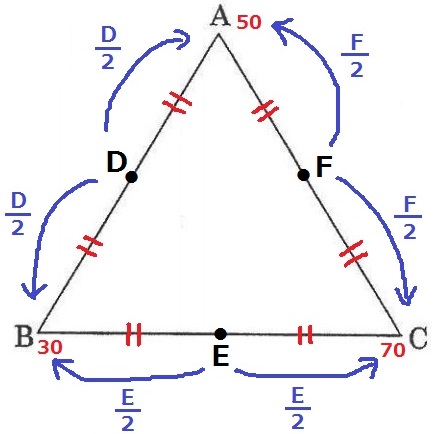
Ｄ・Ｅ・Ｆに置いたおもりの重さは両サイドの頂点に半分ずつ配分される。
Ａ＝Ｄ/２＋Ｆ/２＝50　…①
Ｂ＝Ｄ/２＋Ｅ/２＝30　…②
Ｃ＝Ｅ/２＋Ｆ/２＝70
①を２倍すると、Ｄ＋Ｆ＝100　…③
②を２倍すると、Ｄ＋Ｅ＝60　…④

また、板全体にかかる重さは、Ｄ＋Ｅ＋Ｆ＝Ａ＋Ｂ＋Ｃ＝50＋30＋70＝150　…⑤
③、⑤より、Ｅ＝150－100＝50
④、⑤より、Ｆ＝150－60＝90
Ｄ＝150－（50＋90）＝10
Ｄに10ｇ、Ｅに50ｇ、Ｆに90ｇ置けばいい。

＠別解＠

Ａ＋Ｂ－Ｃ
＝（Ｄ/２＋Ｆ/２）＋（Ｄ/２＋Ｅ/２）－（Ｅ/２＋Ｆ/２）＝Ｄ
Ｄ＝50＋30－70＝10ｇ
ようは、Ｄの両隣り（Ａ50とＢ30）を足して対角（Ｃ70）をひく。

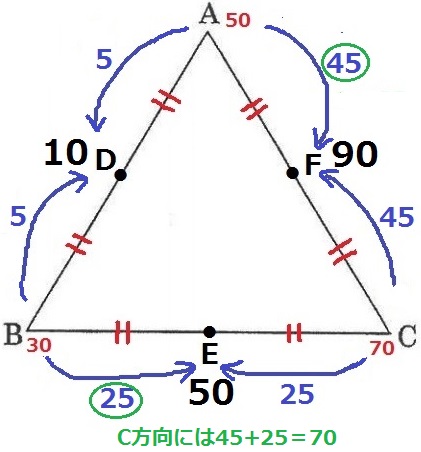
考え方としては、以下の感じだと思う。
辺ＡＢ上にあるＤはＡとＢから影響を受け、Ｃからの影響は受けない。
ＡとＢから捉えるとこれらの一部がＤに集まるが、残りのＡとＢはＣ方向（ＥやＦ）に向かい、
向かった分の和がＣ70ｇに相当するので、Ｄ＝50（Ａ）＋30（Ｂ）－70（Ｃ）＝10ｇが成り立つ。

同様に、Ｅ＝Ｂ＋Ｃ－Ａ＝30＋70－50＝50ｇ
Ｆ＝Ａ＋Ｃ－Ｂ＝50＋70－30＝90ｇ
難関中学（理科）解説ページに戻る