2018年度　江戸川学園取手中学過去問【算数】大問７解説

問題ＰＤＦ
下の図のような直方体があります。
ＡＢ＝８ｃｍ、ＡＤ＝12ｃｍ、ＡＥ＝18ｃｍであるとき、次の問いに答えなさい。

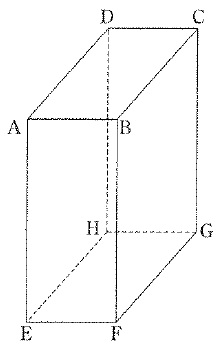
（１）
辺ＢＦ上に点Ｐ、辺ＣＧ上に点Ｑ、辺ＤＨ上に点Ｒをとります。
この直方体の表面上に、ＡからＰ、Ｑ，Ｒを通りＥまで、
距離がいちばん短くなるように線を引きます。
このとき、ＦＰの長さは何ｃｍですか。

（２）
辺ＥＦ上に点Ｓ、辺ＨＧ上に点Ｔ、辺ＤＣ上に点Ｕをとります。
この直方体の表面上に、ＡからＳ、Ｔ，Ｕを通りＢまで、
距離がいちばん短くなるように線を引きます。
このとき、ＥＳの長さは何ｃｍですか。

（３）
直方体の面ＣＤＨＧ上において、（１）で引いた線と（２）で引いた線が交わる点をＯとします。
このとき、ＯＲ：ＯＱを答えなさい。
答えだけでなく、途中の計算や思考過程も書きなさい。

（４）
（１）の点Ｒ、（３）の点Ｏ、直方体の頂点Ｅの３点を通る平面でこの立体を切断するとき、
Ａを含む立体の堆積は何ｃｍ³ですか。

＠解説＠
（１）
最も距離が短い→展開図で直線。

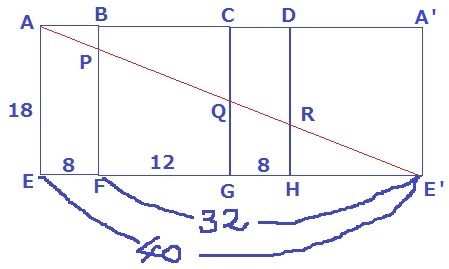
△ＡＥＥ’∽△ＰＦＥ’より、
ＰＦ＝18×32/40＝72/５ｃｍ
頻出のパターンなので必答。

（２）
同じ。縦方向になっただけ。

少々書きにくい(;`ω´)
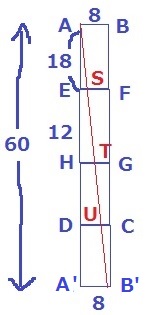
△ＡＡ’Ｂ’∽△ＡＥＳより、
ＥＳ＝８×18/60＝12/５ｃｍ

（３）
（１）と（２）を合体!!(σ’д’)σ

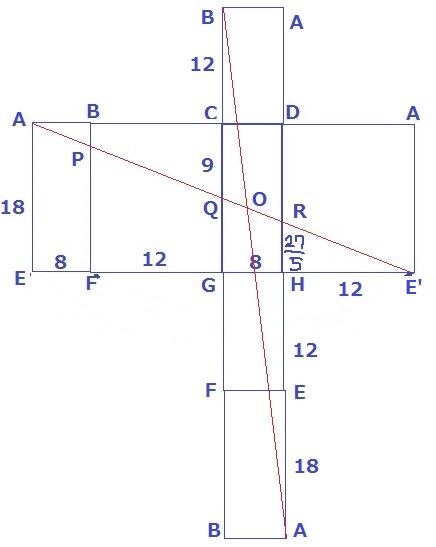
作図に失敗すると、Ｏの位置がズレるので注意。
△ＡＥＥ’∽△ＲＨＥより、
ＲＨ＝18×12/60＝27/５
また、ＱはＡＥ’の半分なのでＣＧの中点にある→ＣＱ＝９

△ＯＲＡ∽△ＯＱＢより、
ＯＲ：ＯＱ＝ＲＡ：ＱＢ
＝27/５＋12＋18：12＋９
＝59：35

（４）

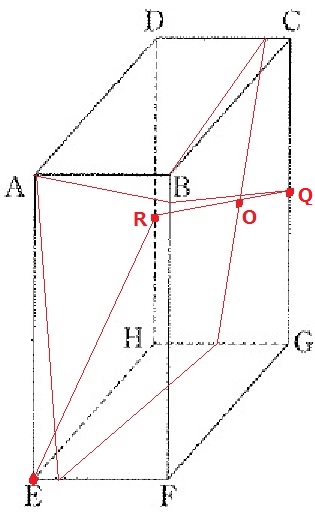
Ｒ・Ｏ・Ｅで切断する。
ということは、ＲＯの延長線上にあるＱも切られる。

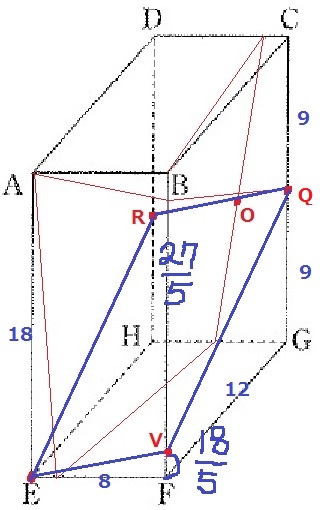
ＲからＥは下へ27/５移動する。
切断面とＢＦとの交点をＶとすると、
ＱからＶも平行して27/５下がる。
ＶＦ＝９－27/５＝18/５
下の立体の体積を求める。
（底面積）×（高さの平均）
＝（８×12）×{（27/５＋９＋18/５＋0）÷４}
＝８×12×９/２

よって、Ａを含む立体の体積は、
８×12×18－８×12×９/２
＝８×12×（18－９/２）
＝８×12×27/２
＝1296ｃｍ³
難関中（算数科）解説ページに戻る