問題PDF
体育館で学年集会を行うことになりました。9人がけの長いすを使って、全員が前から順に着席していきます。ただし、人と人の間隔を1メートル以上空ける必要があるため、9人がけの長いすには1つおきにしか座れません。図1のように5人ずつ座ると長いすの数が少なくてすみますが、図2のように前から5人、4人、5人、・・・と交互に座ると長いすと長いすの間隔をせまくできます。
このとき、次の問いにこたえなさい。

(1) 得点率69.6%
学年の生徒数が240人のとき、図2のように座ると、
図1のときに比べて長いすは何脚多く必要ですか。
(2) 得点率28.9%
学年の生徒数が〔 〕人のとき、図1のときと図2のときの長いすの数の差が3脚で、
どちらも最後列の長いすに座る人数が4人でした。
〔 〕に入る数として考えられるものをすべて答えなさい。
なお、この問題は解答までの考え方を表す式や文章・図などを書きなさい。
(3) 得点率1.4%
図1のときと図2のときの長いすの数の差が4脚のとき、
考えられる生徒数として最も少ないのは何人ですか。
@解説@
差集め算。
(1)

図1は、240÷5=48脚
図2は2脚で1セット(9人)ととらえる。
240÷9=26セット…6人
6人の配分は5人+1人で2脚。
26×2+2=54脚
差は、54-48=6脚
@別解@
2脚1セットで1人の差が生まれる。
図1で48脚だから、48÷2=24人の差が生まれる。
この24人を図2のやり方で座らせると、24÷9=2セット…6人
差は、2×2+2=6脚
(2)

最後列は4人。
図1より生徒数は〔5の倍数+4〕人である。
図1の脚数が偶数個の場合、図2の最後の3脚には5人―4人―4人が座ることになる。
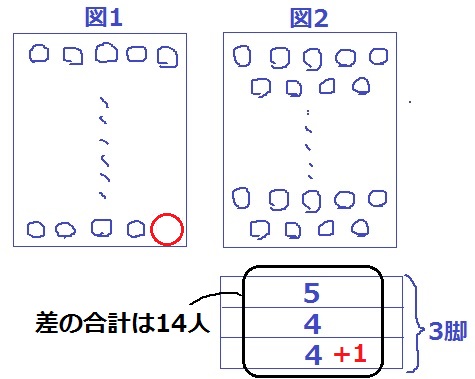
もう1人いると図1の長方形がすべて埋まるのでやりやすくなる。
そこで、生徒数が1人多い場合を想定する。
図2の最後列は5人席だから、1人増えても脚数に変動はない。
同じ脚数における差の合計は、5+4+4+1=14人
2脚1セットで1人の差が生まれるので、図1は1×2×14=28脚
実際の人数は1人少ないから、5×28-1=139人
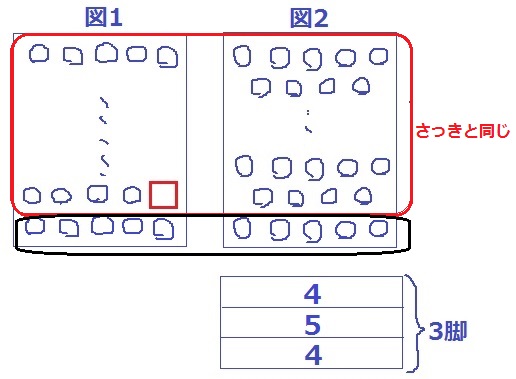
もう1つのシナリオは、図1の脚数が奇数個の場合。
図2の最後の3脚は4―5―4人が座ることになる。
⇒先ほどの5―4―4人と差の合計が変わっていない。
図1の4人は最後列だが、順番を入れ替えて1個手前の列を4人にすると、
上の部分も先ほどと変わらない。
図1と図2に1列5人を足しても変化しない。139+5=144人
144+5=149人にすると差が1人増えるので、もう1脚足さなければならなくなる。
よって、139人と144人。
(3)
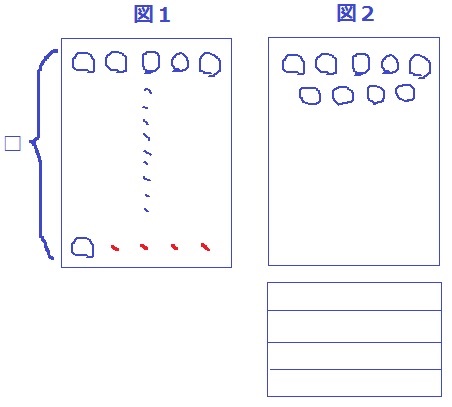
生徒数を少なくするので、図1の脚数□をできるだけ少なくする。
脚数を少なくするということは、図1と同じ脚数における生徒数の差を減らす。

図1は多めにして最後列を5人フルで座らせる。
図2のラスト4列に座る生徒数を少なくするために最後列は1人にする。
手前の3列は5―4―5より4―5―4の方が人数が少ない。
差の合計は4+5+4+1=14人
2列1セットで1人の差を生むから、セットの部分は1×2×14=28列
図2の最後から5列目は5人なので、全体は奇数列だからもう1列ある。
□=28+1
図1より、生徒数は5×29=145人
@余談@

前問の144人の図から答えがすぐでてしまう。
上の図1の□(空席)に1人追加すると、
図2はもう1脚必要になって差が4脚になる。
144+1=145人



コメント