問題PDF
1辺の長さ6cmの立方体があります。立方体の3つの頂点を通る平面で切り、立方体から1つの三角すいを取り除いた、図1のような立体Aを作りました。次の問いに答えなさい。ただし、すい体の体積は、「(底面積)×(高さ)÷3」で求めることができます。

(1)
解答用紙に立体Aの展開図の一部がかかれています。
展開図の1つを完成させなさい。
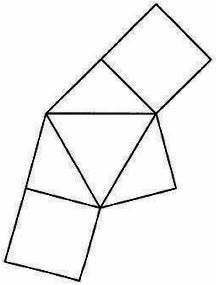
(2)
立体Aの①の面を底面として机に置き、真上から見ると1つの平面図形に見えました。
そのときの図形の名前を答えなさい。
1辺の長さが10cmの立方体があります。立方体の3つの頂点を通る平面で切り、立方体から三角すいを取り除いた後、さらに立方体の3つの頂点を通る別の平面でもう一度切り、三角すいを取り除いた、立体Bを作りました。図2は立体Bの展開図です。ただし、図の等しい印は、等しい長さであることを表しています。

(3)
立体Bの体積は何cm3ですか。
(4)
立体Aを①の面を底面として机に置き、立体Bを②の面を底面として机に置きます。
このときの、立体Aと立体Bの高さの比を最も簡単な整数の比で表しなさい。
@解説@
(1)
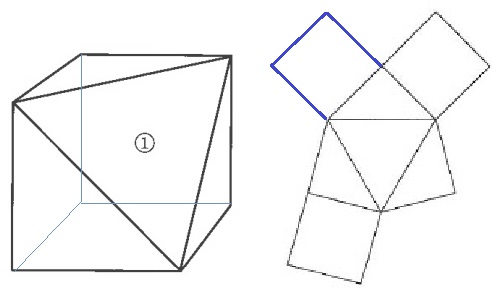
7面あって、足りないのは正方形。
正しい位置にあれば、どこでも正解。
(2)
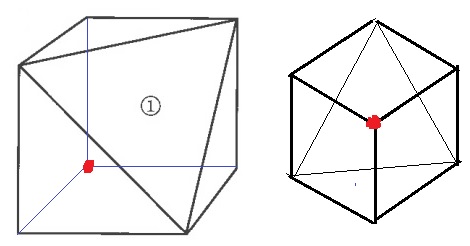
奥にあった、3つの正方形の角が集まる●が一番上にくる。
●を中心に真上から眺めると、右のように3つの正方形が正六角形のように見える。
(3)
立方体の1辺の長さが、6cmから10cmに変わっていることに注意。

先ほどの切断から、さらにもう1回切断すると左の展開図となった。
ポイントは点対称。切断部分も点対称となり、同じような三角錐で反対側も切断する。
10×10×10-10×10÷2×10÷3×2=2000/3cm3
(4)
2つの立体の高さの比を求める。
底面を下にした作図は手間がかかるので、そのままの状態から高さの比を考えてみよう。
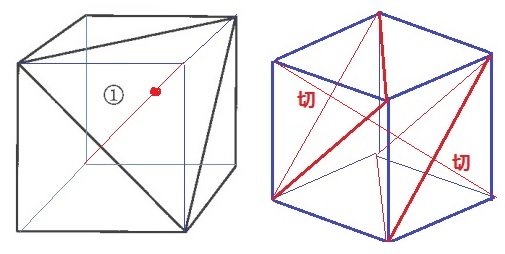
辺の長さは違うが、底面とする正三角形は切断の仕方が同じ。
立方体の対角線に注目しよう。
立方体の大きさが違うので、対角線の長さも違うが、
この対角線は立方体の頂点を結ぶので、立方体と対角線の位置関係は2つとも変わらない。

面AEGCを正面にして関係性を捉えよう。
断面を底面としたとき、OEは高さにあたらないが、
求めたいのは”高さの比”なので、OEの長さとの比が答えになりうる。
△BOC∽△GOE(∽=相似)より、EO:OC=2:1
1辺6cmの立方体で、高さの比OEは対角線の2/3倍。

同様に、面AEGCで捉える。
△ABP∽△GEP、△ACQ∽△GFQなどから、
AP:PQ:QG=1:1:1
1辺10cmの立方体で、高さの比PQは対角線の1/3倍。
立体Aの高さ:立体Bの高さ=6×2/3:10×1/3=4:10/3=6:5



コメント