問題ＰＤＦ
Ｋ中学校の冬期講習は、１日６時間で、国語、数学、英語、
各２時間の授業があります。次の問いに答えなさい。
（１）
時間割の作り方は全部で何通りありますか。
（２）
同じ科目の授業は２時間連続しないことにすると、時間割の作り方は全部で何通りありますか。
（３）
講習の希望者が多くなり、クラスをＡ組とＢ組の２つに分けて授業を行うことになりました。
Ａ組とＢ組で同じ時間に同じ科目の授業は行われません。
このとき、時間割の作り方は全部で何通りありますか。
ただし、同じ科目の授業が２時間連続してもよいことにします。
＠解説＠
（１）
国語、数学、英語をＡ、Ｂ、Ｃに置きかえると、
ＡＡＢＢＣＣの並び替えの問題に帰結する。
６×５×４×３×２×１÷（２×１）÷（２×１）÷（２×１）
＝90通り
（２）
ＡＡＢＢＣＣが隣り合わない場合の数を求める。
先にＡＡＢＢの並び方は、４×３×２×１÷（２×１）÷（２×１）＝６通り
６通りに場合分けして、残りのＣの位置を決めていく。
・【ＡＢＡＢ】と【ＢＡＢＡ】
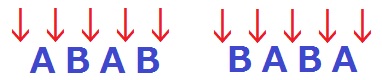
あいだの↓に２つのＣを挿入する。
5Ｃ２×２＝20通り
・【ＡＡＢＢ】【ＢＢＡＡ】
Ｃの位置が確定する。合計２通り。
・【ＡＢＢＡ】【ＢＡＡＢ】
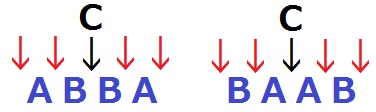
１つのＣは確定。もう１つのＣを４つの↓から選ぶ。
4Ｃ1×２＝８通り
したがって、20＋２＋８＝30通り
（３）
Ａ組だけだと、（１）より90通り。
Ａ組が【ＡＡＢＢＣＣ】のとき、Ｂ組は何通りあるか。
１時間目と２時間目の組み合わせで場合分けする。
Ａ・Ｂ・Ｃの並びには対称性があり、文字の場所を入れ替えても全体の様子が変わらない。
【ＢＢ】１通りとわかれば、【ＣＣ】も１通り、
【ＢＣ】４通りとわかれば、【ＣＢ】も４通りである。
合計10通り。
全部で、90×10＝900通り
難関中（算数科）解説ページに戻る
コメント