問題ＰＤＦ
（１）
図の長方形で、ＡＢの長さが５ｃｍのとき、角アの大きさは角イの大きさを
〔 〕倍して60度を加えたものです。〔 〕にあてはまる数を答えなさい。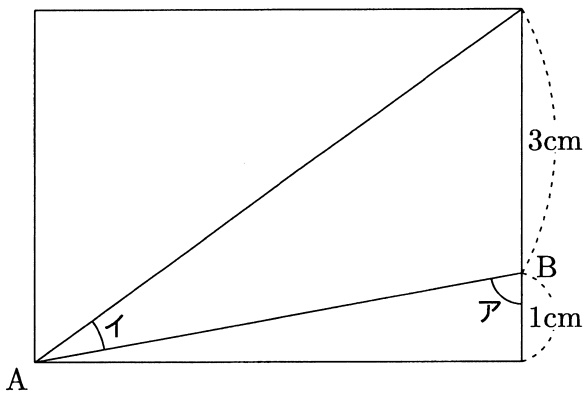
（２）
図の点Ａから点Ｂまで、半径１ｃｍの円が転がります。
円が通った部分の面積は何ｃｍ2ですか。
（３）
図の立体は、１辺６ｃｍの正方形１枚と、底辺の長さが６ｃｍ、高さが４ｃｍの二等辺三角形４枚を組み立ててできます。３点Ｏ、Ｅ、Ｆを通る平面で２つの立体に切り分けるとき、表面積の差は何ｃｍ2ですか。
＠解説＠
（１）
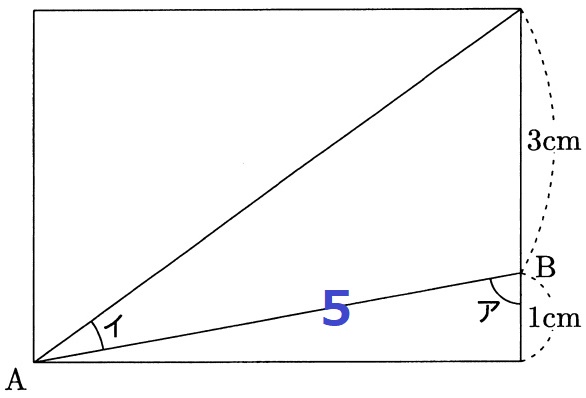
妙な５ｃｍをどう使うべきか。
長方形の縦の長さが４ｃｍ…もう１ｃｍ足せば５ｃｍが作れる。
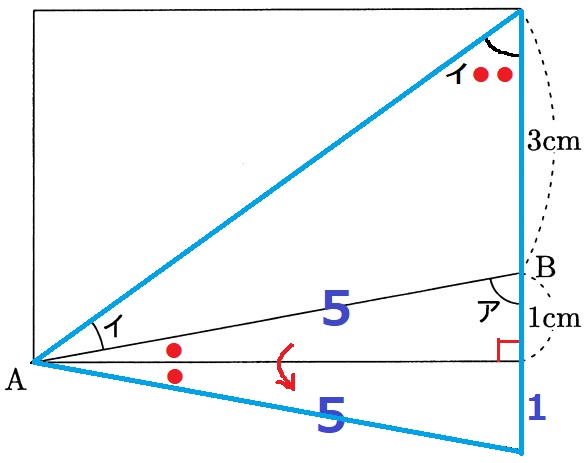
そこで、直角三角形を下にクルッとひっくり返してみる。
水色の三角形は等辺５ｃｍの二等辺三角形。
折り返した直角三角形の最も小さい角を●とする。
二等辺の底角はイ●●となる。
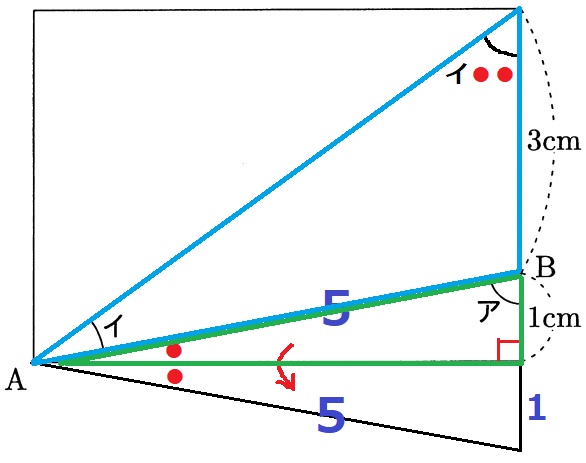
水色の三角形の外角定理で、イイ●●＝ア
また、緑色の直角三角形の内角より、●＝90－ア
これを手前の式の●にあてはめると、
イ＋イ＋（90－ア）＋（90－ア）＝ア
イ×２＋180－ア×２＝ア
ア×３＝イ×２＋180
ア＝イ×２/３＋60
アの大きさはイを２/３倍して60度を加えたもの。
２/３
（２）
正確に作図する。
求積すべき図形は青線で囲んだところ。
①半径１ｃｍの円
②半径２ｃｍの円
③縦２ｃｍ、横（４×６＋２×２）＝28ｃｍの長方形
④円が通らない斜線部分を引く。１辺２ｃｍの正方形から半径１ｃｍの円を引いたもの。
したがって、１×１×3.14＋２×２×3.14＋２×28－（２×２－１×１×3.14）
＝６×3.14＋52＝70.84ｃｍ2
（３）
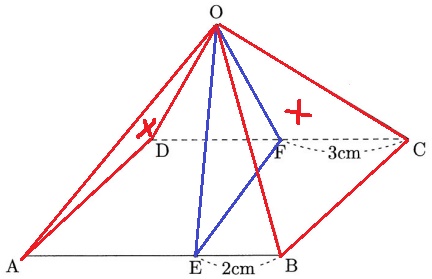
求めたいのは表面積の差なので、等しい面積を相殺していく。
断面の△ＯＥＦは左右同じ。
正四面体の側面である△ＯＡＤと△ＯＢＣは合同で相殺。
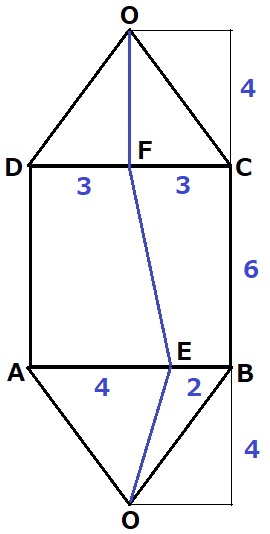
残り３面の展開図を描く。左右の表面積の差が答え。
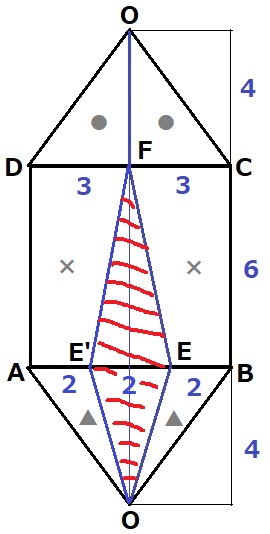
図形全体が線対称。
ＦＥとＥＯを対称移動させると、●×▲が対称図形で合同。
これらを相殺すると、表面積の差は斜線部分にあたる。
２×10÷２＝10ｃｍ2
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント