問題PDF
高さが同じで、底面積の異なる2つの子どもプールA、Bがあります。
ある日、空になっている2つのプールに、毎分12Lの割合で水が出るホースをそれぞれ1本ずつ入れ、同時に水をため始めました。Aの水面の高さが満水のちょうど半分になったとき、Bの水面の高さはAの水面の高さより6cm低く、Aの水面の高さが満水まであと9cmになったとき、Bの水面の高さはAの水面の高さより9cm低くなっていました。
その後、Aが満水になるとすぐに、Aに入っていたホースもBに入れ、それ以降はBに2本のホースを使って水を入れました。水をA、Bにため始めてから60分後にBも満水になりました。
プールの側面や底面の厚さは考えないものとして、次の問いに答えなさい。
(1)
プールAとプールBの底面積の比を最も簡単な整数の比で答えなさい。
(2)
プールの高さは何cmですか。
(3)
プールAの底面積は何cm2ですか。
@解説@
(1)(2)
*(2)が先に判明する。
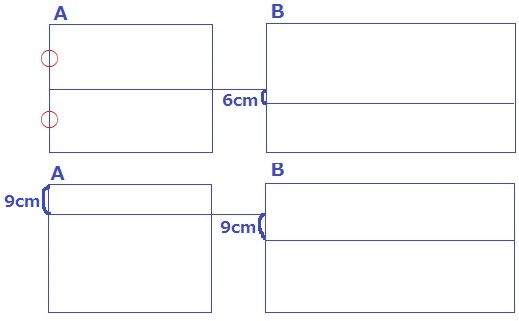
先にAが満水になるので、Bの方が底面積は大きい。
差が6cmから9cmに拡大している。
時間と共に差は比例で拡大するので、高さの差の比は時間の比にあたる。
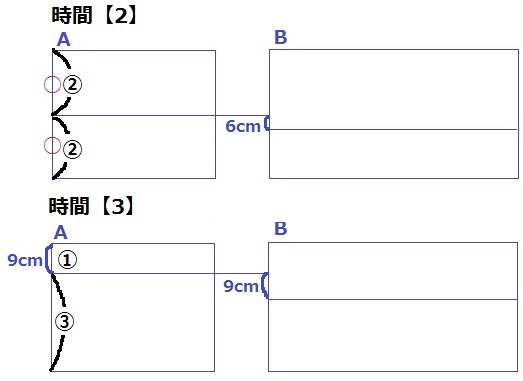
時間の比は、6:9=【2】:【3】
時間【2】のときのAの高さを②、時間【3】のときを③とする。
水槽の高さは②×2=④
ということは、9cmの部分が④-③=①にあたる。
水槽の高さは、9×④=36cm
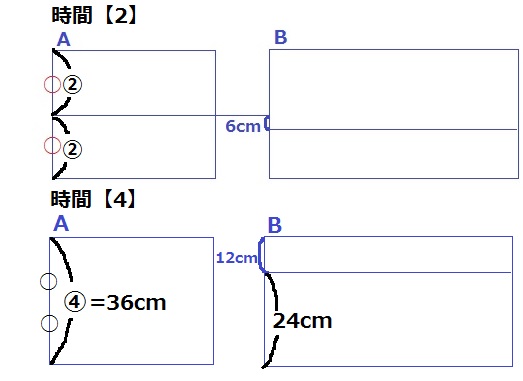
Aの高さが水槽の半分に達した時間【2】で、差は6cm。
Aが満水になる時間【4】では、差は12cmに広がる⇒Bの高さは24cm。
底面積の比は高さの逆比。
A:B=24:36=2:3
(1)2:3、(2)36cm
(3)
水槽の高さはわかっている。
Aの底面積を知るには、Aの容積が知りたい。
Aの容積を知るには、Aが満水になった時間が知りたい。
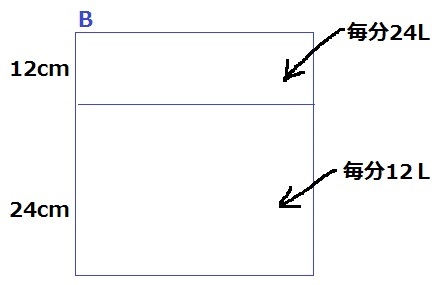
時間の情報は【Bの満水が60分後】
Bが高さ24cmに達したとき、Aは満水になった。
60分のうち、下部分が埋まったのは何分後か。

速さと同じように考えるとわかりやすい。
容積を距離、流量を速さとみなす。
距離(容積)の比は、上:下=12:24=【1】:【2】
時間の比は速さ(流量)の逆比。上:下=12:24=①:②
これは距離(容積)が一定の場合の時間の比なので、
実際の時間の比は、上:下=①×【1】:②×【2】=1:4
下部分の時間は、60×4/5=48分
12L=12000cm3だからAの底面積は、12000×48÷36=16000cm2



コメント