問題ＰＤＦ
（４）
１から９までの整数から７つ選んで、それぞれａからｇとします。
下のような式が成り立つたとき、ｅは〔 〕、ｆは〔 〕、ｇは〔 〕です。
ａ×ａ＝ｂ ｃ＋ｄ＝ａ
ｃ×ｅ＝ｆ ｃ＋ｇ＝ｆ
（５）
１Ｌサイズの牛乳パックの重さは50ｇです。
これを１個リサイクルすることで、二酸化炭素の排出量を23.4ｇ削減できます。
また、二酸化炭素14ｋｇは１本の杉の木が吸収する二酸化炭素と同じです。
ある年の国内の牛乳パックのリサイクル量は68.5千ｔでした。
この年の二酸化炭素削減量は、約〔 〕万本分の杉の木が吸収する二酸化炭素量に相当します。
（小数第１位を四捨五入すること）
（７）
三角形ＡＢＣの面積は10ｃｍ2です。
図のように三角形ＡＢＣの辺ＣＡをＡの方に延長してＣＡ：ＡＤ＝１：２となるように
点Ｄをとります。同じように、ＡＢ：ＢＥ＝１：３、ＢＣ：ＣＦ＝１：４となるように
それぞれ点Ｅ、Ｆをとり、三角形ＤＥＦを作りました。
三角形ＤＥＦの面積は〔 〕ｃｍ2です。
（８）
図のように３つの円柱状の容器（ア）（イ）（ウ）があります。
底面の半径は、（イ）は（ア）の２倍、（ウ）は（イ）の1.5倍で、
高さは、（イ）は（ア）の1.5倍、（ウ）は（イ）の1.5倍です。
（イ）を満水にして空の（ウ）に何回か水を入れたところ、水があふれてしまいました。
このとき、あふれた水の量は（ア）の〔 〕杯分です。
（９）
ある中学校の生徒が一列に並んでハイキングコースを歩いています。
最後尾にいた守くんが1.8ｋｍ先の先頭まで走って行ったところ、
９分で先頭に着くことができましたが、先頭にいた先生に最後尾に戻るよう指示されました。
そこで、守くんはその場で列が過ぎるのを待っていると、27分で最後尾になりました。
もし、守くんが行きと同じ速さで戻ったならば〔 〕分〔 〕秒で最後尾に着きます。
（11）
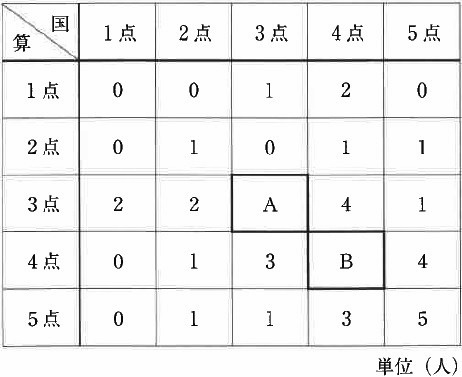
あるクラスで５点満点の国語と算数のテストを行ったところ、
得点の分布が下の表のようになりました。
国語の平均点が3.6点、算数の平均点が3.5点のとき、
ＡとＢに入る人数は、Ａ〔 〕人、Ｂ〔 〕人です。
（12）
図のように、中心角が90度のおうぎ形を点線で２回折りました。
（あ）の大きさは〔 〕度です。
（14）
表は、あるクラスの算数のテストの結果です。
このテストは第１問が10点、第２問が５点、第３問が５点の20点満点です。
第１問を正解した人は22人、第２問を正解した人は17人いました。
①第２問と第３問の両方を正解した人は〔 〕人です。
②第３問を正解した人は〔 〕人です。
＠解説＠
（４）
１～９の中で、ａ×ａ＝ｂが成り立つ組み合わせを考える。
（ａ、ｂ）＝（２、４）（３、９）
ｃ＋ｄ＝ａで、ａ＝２だと１＋１になり、ｃ、ｄと別のアルファベットにならない。×
ａ＝３、ｂ＝９確定
ｃ＋ｄ＝３となり、（ｃ、ｄ）＝（１、２）（２、１）
ｃ×ｅ＝ｆで、ｃ＝１だとｅ＝ｆとなるから不適。
ｃ＝２、ｄ＝１確定
２×ｅ＝ｆ、２＋ｇ＝ｆで、残りの数字をあてはめる。
ｅ＝４、ｆ＝８、ｇ＝６
（５）
桁ミスに気をつけて計算するだけだが、苦手な人は多い。
68.5千ｔ（牛乳パックリサイクル量）÷50ｇ（牛乳パック１本）＝リサイクルした牛乳パックの本数
これに23.4ｇをかければ、リサイクルで削減できたＣＯ2の量となる。
それを÷14ｋｇで杉の本数に換算して、÷１万で杉何万本かがでる。
68.5千ｔ÷50ｇ×23.4ｇ÷14ｋｇ÷１万
＝68.500.000.000÷50×23.4÷14.000÷10.000
＝137×23.4÷14＝228.9‥ →229万本
精神力が試される・・(( ;ﾟдﾟ))
大きな数は３桁ごとに点を打った方がいいかも。
（７）
補助線をひいて、サクサク調べていく。
△ＤＥＦ＝360ｃｍ2
（８）
基本レベルなのできちんと正解したい。
ア：イ：ウ
半径 ＝１：２：３
底面積＝１：４：９
高さ ＝１：1.5：2.25
体積 ＝１：６：20.25
イをウに入れると、３回まではセーフだが、４回目でこぼれる。
その量は、６×４－20.25＝3.75
これは、アの3.75杯分。
（９）
旅人算。せっかく先頭にきたのに戻される(._.)
1800ｍ÷（太郎の速さ－行列の速さ）＝９分
太郎の速さ－行列の速さ＝分速200ｍ
行列の速さ＝1800ｍ÷27＝分速200/３ｍ
よって、太郎の速さ＝200＋200/３＝分速800/３ｍ
求める答えは、1800÷（太郎の速さ＋行列の速さ）
＝1800÷（800/３＋200/３）＝５・2/5＝５分24秒
（11）
ＡとＢ以外のマスの合計を算出。
国語…１×2＋2×4＋3×5＋4×10＋5×11＝122
算数…１×3＋2×3＋3×9＋4×8＋5×10＝118
ＡＢ以外のマスの合計差が122－118＝４点
Ａは国算がともに３点のマス、Ｂはともに４点のマス。
ということは、ＡＢ以外のマスの合計差が、そのまま国語と算数の合計差となる。
国語と算数の平均点の差は0.1点。
平均の差×人数＝合計の差
人数＝４÷0.1＝４０人
国語の合計は、3.6×40＝144点
ＡとＢのマスの国語の得点は、144－122＝22点
ＡとＢの人数は、40－33（表をもとに地道に数える）＝７人
３×Ａ＋４×Ｂ＝22で、ＡとＢの和が７になる組み合わせを求める。
Ａ＝６人、Ｂ＝１人
処理手順が多いので、時間にとられる。。
後回しでも良いかな？
（12）
１回目は、扇形の中心角が孤の上にくるように折る。
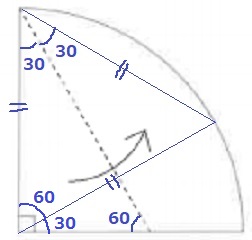
半径と折り返しから、正三角形が現れる。
30－60－90°の直角三角形がみつかる。
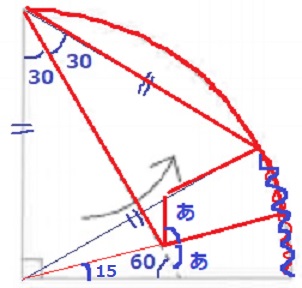
２回目は波線の孤を半分に折り、
右下の点が１回目に折ったときの点に重なるようにする。
角の二等分線で15°。折り返しで（あ）を移動。
外角定理から、60＋15＝75°
（14）①
ラストに推論問題。
第１問～第３問をそれぞれ①、②、③とおく。
20点…全問正解→①②③＝４
15点…①②or①③＝13
10点…①or②③＝８
５点…②or③＝６
ベン図で情報整理。
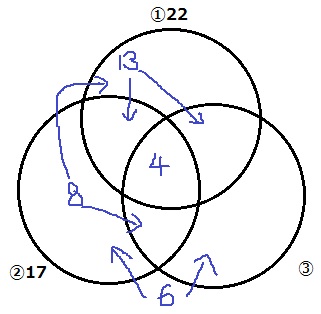
↑こうなる。
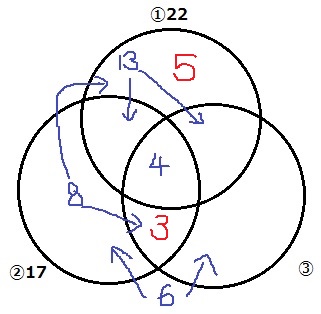
①の円に注目すると、①だけ正解した人は、
22－13－４＝５
②と③だけを正解した人は、８－５＝３
よって、②と③を両方正解した人は７人。
②
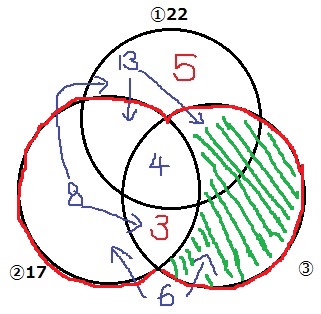
②と③の合計（赤い枠）は、
13＋４＋３＋６＝26
ここから②を引いて、緑の斜線部分を求める。
26－17＝９
③の正解者は、９＋４＋３＝16人
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント