問題ＰＤＦ
（１）
短針と長針が下の図１のように折れ曲がった時計があります。
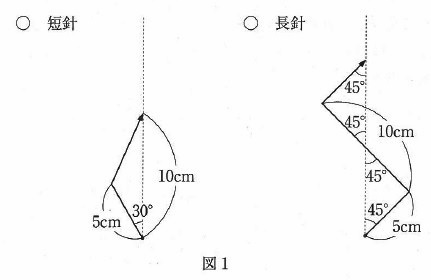
例えば「６時00分」には下の図２のようになります。このとき、６時から７時の間で、短針と長針の一部が重なっている時刻は６時何分何秒から６時何分何秒までか求めなさい。ただし、秒の値は分数で答えなさい。
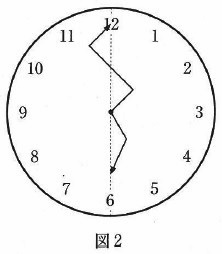
（２）
例のように立体図形を上から見て反時計回りに90°回転移動させた図形を考えます。
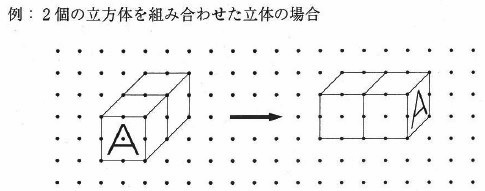
下の図のような５個の立方体を組み合わせた立体を上から見て反時計回りに90°回転させた図形を解答欄に図で表しなさい。ただし、「Ａ」とかいてある面だけは示してあるので、残りの部分を表しなさい。また、見えない部分の線はかかないこととします。
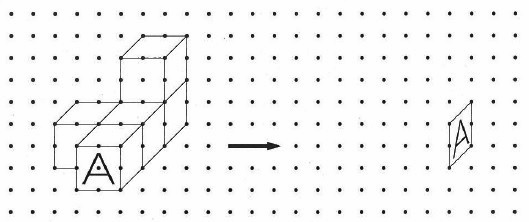
＠解説＠
（１）
１分間に長針は360÷60＝６°、短針は30÷60＝0.5°
１分あたり、６－0.5＝5.5°近づいていく。
長針と短針が離れている角度を求める。
長針が初めて短針に追いつくのは105°移動したとき。
105÷5.5＝210/11＝19・１/11分
60×１/11＝60/11＝５・５/11秒
19分５・５/11秒
問題は長針が短針を追い越すとき。
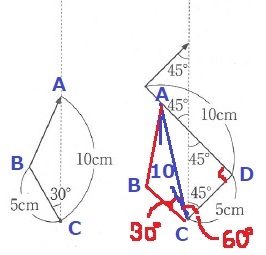
図１は短針と長針の針の向きがともに上方向なので、この図で考えてみる。
短針の３点をＡ・Ｂ・Ｃとする。
Ａが長針に接するように、ＡＣを傾ける。
すると、△ＡＣＤはＡＣ：ＣＤ＝２：１の直角三角形で、∠ＡＣＤ＝60°となる。
文字盤だとこうなる。長針のスタート地点から180－45＋60＝195°と離れている。
195÷5.5＝35・５/11分
60×５/11＝27・３/11秒
35分27・３/11秒
したがって、６時19分５・５/11秒から６時35分27・３/11秒まで。
（２）
ここはみんな正解してくるので、ケアレス注意です。
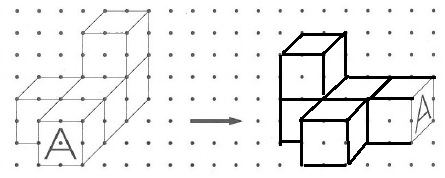
１辺２目盛り、斜めは１×１の正方形の対角線。
見えない部分に破線は書かないこと。
難関中（算数科）解説ページに戻る
コメント