2020年度　東京都市大学付属中学過去問【算数】大問４解説

問題ＰＤＦ
下の図のように、角Ａと角Ｃが直角で、ＡＢ＝ＡＤである四角形ＡＢＣＤがあります。
辺ＡＢのちょうど真ん中の点をＥとして、Ｅを通りＢＣに平行な直線はちょうどＤを通ります。
また、Ｆは辺ＢＣのちょうど真ん中の点で、ＡＤとＢＣをそれぞれのばし、
交わった点をＧとします。あとの問いに答えなさい。

問１
（三角形ＡＢＧの面積）：（三角形ＤＣＧの面積）を最も簡単な整数の比で表しなさい。

問２
（三角形ＡＦＤの面積）：（四角形ＡＢＣＤの面積）を最も簡単な整数の比で表しなさい。

＠解説＠
問１
問題文に数字が一切書かれていない！

Ｆは関係ないので、ＡＦとＤＦを消した。
ＡＥ＝ＥＢ＝〇とする。
ＡＢ＝ＡＤから、ＡＤ＝〇〇
ＥＤ//ＢＧより、△ＡＥＤ∽△ＡＢＧ（∽…相似）
ＡＥ：ＥＢ＝１：１から、ＡＤ：ＤＧ＝１：１（ＤはＡＧの中点）
ＤＧ＝〇〇
△ＡＢＧと△ＤＣＧは、直角と共通角で２角が等しく相似。

直角三角形ＡＢＧの辺の比で、ＡＢ：ＡＧ＝１：２
これと相似にある△ＤＣＧの辺でＤＣ＝①、ＣＧ＝②とおく。

ＡからＢＧに向けて垂線、その足をＨとし、ＡＨとＥＤの交点をＩとする。
△ＡＩＤと△ＤＣＧは１辺と両端角が等しく合同→ＡＩ＝①、ＩＤ＝②

△ＢＡＨも△ＡＩＤと２角が等しく合同で、ＢＨ：ＨＡ＝①：②となる。
四角形ＩＨＣＤは①×②の長方形。
うえのように△ＡＢＧを分割すると、△ＡＢＧ：△ＤＣＧ＝５：１

問２
△ＡＦＤを調べるので、Ｆに注目する。

前図でＢＣ＝③だったので、ＢＦ＝ＦＣ＝〇1.5
△ＤＣＧの面積を②×①÷２＝【１】とすると、
問１の答えから△ＡＢＧの面積は【５】、四角形ＡＢＣＤの面積は【４】となる。

△ＡＢＦ…〇1.5×②÷２＝【３/２】
△ＤＦＣ…〇1.5×①÷２＝【３/４】
△ＡＦＤ…【４】－【３/２】－【３/４】＝【７/４】
△ＡＦＤ：四角形ＡＢＣＤ＝７/４：４＝７：16

＠＠

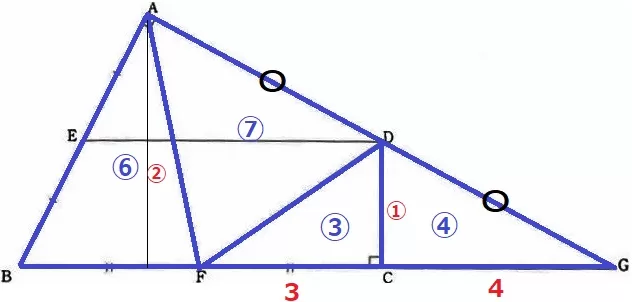
ＦＣ：ＣＧ＝３：４とわかれば、このように整理できました。
△ＤＦＣ：△ＤＧＣ＝③：④
△ＡＢＦ＝△ＤＦＣ×２＝⑥
△ＡＦＤ：△ＧＦＤ＝ＡＤ：ＤＧ＝⑦：⑦
難関中（算数科）解説ページに戻る