問題ＰＤＦ
Ａ地点とＢ地点を結ぶ動く歩道があります。
この動く歩道は、Ａ地点からＢ地点に向かって一定の速さで動いています。
太郎君と花子さんがＡ地点からＢ地点まで動く歩道を利用して歩いたところ、
太郎君は１分36秒、花子さんは２分かかりました。
また、太郎君が動く歩道を利用せずにＡ地点からＢ地点まで歩いたところ、
動く歩道を利用して歩いたときよりも32秒多くかかりました。
（１）
太郎君の歩く速さと動く歩道の進む速さの比は、何対何ですか。
（２）
太郎君と花子さんの歩く速さの比は、何対何ですか。
（３）
太郎君と花子さんが、Ａ地点を同時に出発し動く歩道を利用して歩きました。
動く歩道の途中で、太郎君は〔 〕秒間立ち止まったところ、
２人は同時にＢ地点に到着しました。〔 〕にあてはまる数はいくつですか。
＠解説＠
（１）
ＡからＢまで、太郎（歩道あり）は96秒、太郎（歩道なし）は128秒かかる。
時間の比は、96：128＝３：４
速さの比は時間の逆比。
太郎（歩道あり）：太郎（歩道なし）＝④：③
歩道の速さは①なので、太郎（歩道なし）：動く歩道の速さ＝３：１
（２）
太郎（歩道あり）と花子（歩道あり）の速さの比は、
120：96＝⑤：④
この⑤と④に含まれる歩道の速さを抜く。
前問より、太郎（歩道なし）：動く歩道の速さ＝３：１だったので、
太郎（歩道あり）の⑤に含まれる歩道の速さは、⑤×１/４＝○５/４
太郎（歩道なし）＝⑤－○５/４＝○15/４
花子（歩道なし）＝④－○５/４＝○11/４
したがって、太郎（歩道なし）：花子（歩道なし）＝〇15/４：〇11/４＝15：11
（３）
太郎が120秒でＢに着くようにする。
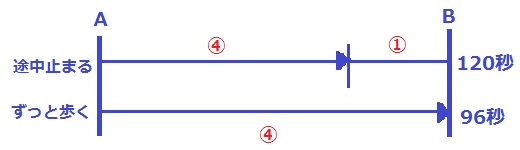
前半に歩いて、後半ずっと止まってＢに着いたとする。
一方、歩道の上をずっと歩いたら96秒で着く。
太郎が歩道の上を歩くと④、止まると歩道の速さ①で進むので…
差の24秒は、後半の部分で起こる。
この部分の時間の比は〔４〕：〔１〕
〔３〕＝24秒なので、止まった時間〔４〕は、24×４/３＝32秒間
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント