2022年度　聖光学院中学過去問【算数】大問５解説

問題ＰＤＦ
（１）
長さ27ｃｍの直線ＡＢ上を、長さ９ｃｍの２直線Ｐ、Ｑが移動することを考えます。

（ア）
図１のように、直線Ｐは左端が点Ａに、直線Ｑは右端が点Ｂにつくようにおかれています。

直線Ｐはある時刻に毎秒１ｃｍで点Ｂに向けて移動を開始し、右端が点Ｂについたら止まります。直線Ｑは、直線Ｐと同時に毎秒２ｃｍで点Ａに向けて移動を開始します。直線Ｑは左端が点Ａについたらすぐに、点Ｂに向けて移動を開始し、右端が点Ｂについたら止まります。
このとき、２直線Ｐ、Ｑが移動を開始してからの時間（秒）と、Ｐ、Ｑが重なっている部分の長さ（ｃｍ）の関係を表すグラフを、解答欄にかき入れなさい。ただし、グラフの横軸の１目盛りは１秒、縦軸の１目盛りは１ｃｍとします。

（イ）
図２のように２直線Ｐ、Ｑがともに左端が点Ａにつくようにおかれています。

直線Ｐはある時刻に毎秒１ｃｍで点Ｂに向けて移動を開始し、右端が点Ｂについたら止まります。直線Ｑは、直線Ｐと同時に毎秒２ｃｍで点Ｂに向けて移動を開始します。直線Ｑは右端が点Ｂについたらすぐに、点Ａに向けて移動を開始し、左端が点Ａについたら止まります。
このとき、２直線Ｐ、Ｑが移動を開始してからの時間（秒）と、Ｐ、Ｑが重なっている部分の長さ（ｃｍ）の関係を表すグラフを、解答欄にかき入れなさい。ただし、グラフの横軸の１目盛りは１秒、縦軸の１目盛りは１ｃｍとします。

（２）
図３のような、１辺の長さが27ｃｍの正方形ＡＢＣＤの中を、１辺の長さが９ｃｍである２つの正方形Ｒ、Ｓが一定の速さで移動することを考えます。

はじめ、正方形Ｒは左下の頂点が点Ａにあり、点Ａを含むＲの２辺と正方形ＡＢＣＤの２辺が重なるようにおかれています。ある時刻に、正方形Ｒは点Ｃに向けて移動を開始します。Ｒの対角線の交点が直線ＡＣ上にあり、Ｒの辺が正方形ＡＢＣＤの辺と平行になるように移動をし、Ｒの右上の頂点が点Ｃにつくまで、18秒間で移動をします。
また、正方形Ｓは右下の頂点が点Ｂにあり、点Ｂを含むＳの２辺と正方形ＡＢＣＤの２辺が重なるようにおかれています。Ｒと同時に、正方形Ｓは点Ｄに向けて移動を開始します。Ｓの対角線の交点が直線ＢＤ上にあり、Ｓの辺が正方形ＡＢＣＤの辺と平行になるように移動をし、Ｓの左上の頂点がＤについたらすぐに点Ｂに向けて移動を開始し、Ｓの右下の頂点が点Ｂにつくまで、18秒間で移動をします。

（ウ）
移動を開始してから５秒後について、２つの正方形Ｒ、Ｓが重なる部分の面積は何ｃｍ²ですか。

（エ）
２つの正方形Ｒ、Ｓが重なる部分が正方形になるのは、移動を開始してから〔　〕秒後です。
（１）のグラフを利用して、〔　　〕にあてはまる数として考えられるものをすべて答えなさい。

＠解説＠
（１）ア

ＰとＱが重なり始めるのは、９÷（１＋２）＝３秒後

後ろの点が出会うまでＰとＱは重なる。18÷（１＋２）＝６秒後
中点同士が重なる３秒後にＰとＱは完全に一致して重なりは９ｃｍ。
その３秒後にＱの左端がＡに着いて、Ｐとの重なりはちょうど０ｃｍとなる。

ここから追いかける展開になる。重なりは徐々に増えていく。
９÷

（２－１）＝９秒後にＰとＱの右端が同時にＢへ到着する。
まとめるとこうなる。

イ

９秒後にＱがＰを完全に追い越したとき、Ｑの右端がＢに着く。
15秒後にＰとＱの重なりが０ｃｍになる。

（２）ウ

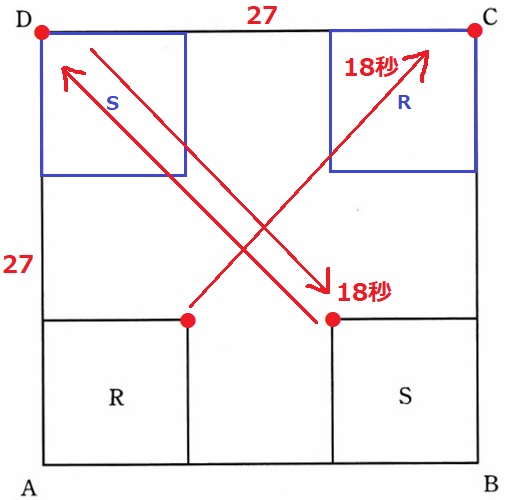
２つの正方形が斜めに移動する。
Ｒの右上の頂点●がＣに到着するまでが18秒。
Ｓの左上の頂点●がＤに着き、再び同じ地点に到着するまでが18秒。
何か見え覚えのある動き。。

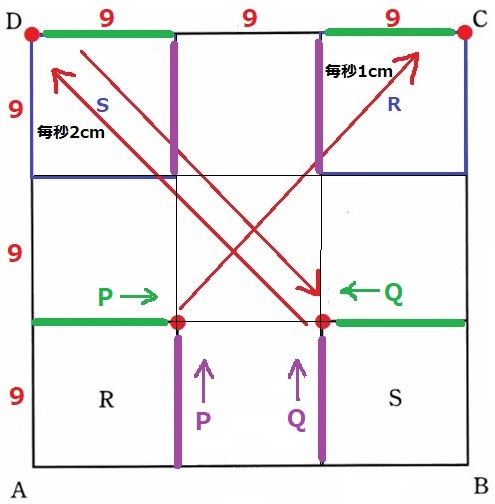
９ｃｍずつで区切って見ると、前問の様子と酷似している。
横の辺（緑）だけを見ると９ｃｍずつで、あいだも９ｃｍ。
毎秒１ｃｍのＲはＣまでだが、毎秒２ｃｍのＳはＤに着いて戻ってくる。
（１）アと一緒！

今度は縦の辺（紫）だけを見る。
最初ＲとＳが同じ位置にあり、毎秒１ｃｍのＲは行きだけだが、
毎秒２ｃｍのＳは行って戻ってくる。（１）イと一緒！！
つまり、（２）は（１）のＰとＱの動きを２次元化したもの。
２つのグラフを重ねて５秒後をみると、４ｃｍと６ｃｍ。
重なる部分の面積は、４×６＝24ｃｍ²

＠余談＠

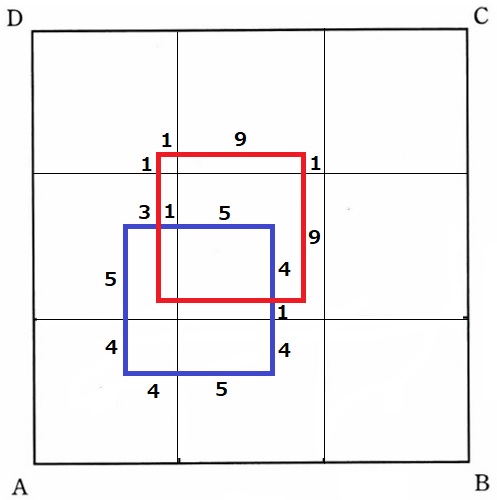
本当か？と疑い深いサボは調べてみました。
４×６＝24ｃｍ²であってました。

エ
仕組みさえわかってしまえば、すぐ解ける。

正方形は縦と横の長さが等しい⇒重なった部分の縦と横の長さが等しい。
０ｃｍでない交点を求めればいい。
上下の合同な三角形に注目して、
３と６の中点→4.5秒後
12と15の中点→13.5秒後
4.5秒後と13.5秒後
難関中（算数科）解説ページに戻る