2019年度　筑波大附属中学過去問【算数】前半１～６解説

問題ＰＤＦ
（１）①
16×0.875－1.6×3.75－0.16×12.5　を計算しなさい。

⑥下の図のように、模造紙をタイトル、地図、名前の３つの部分に分けて、
南北約360ｋｍの九州の地図をかきます。
模造紙の大きさは縦100ｃｍ、横80ｃｍ、かいた地図の縮尺は45万分の１でした。
タイトル部分の縦の長さが名前部分の縦の長さの２倍になるとき、
タイトル部分の縦の長さを選びなさい。

ア：約19ｃｍ　イ：約16ｃｍ　ウ：約13ｃｍ
エ：約10ｃｍ　オ：約７ｃｍ

⑦下の図で、（ア）の角の大きさを求めなさい。
 

（２）②
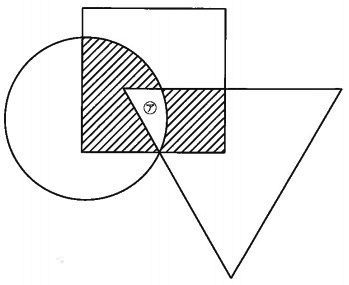
下の図のように、円、正方形、三角形が重なっています。
円、正方形、三角形のそれぞれの面積は70ｃｍ²、図形全体の面積は148ｃｍ²、
３つの図形が重なっている（ア）の部分の面積が７ｃｍ²のとき、
斜線部分の面積を求めなさい。

（３）
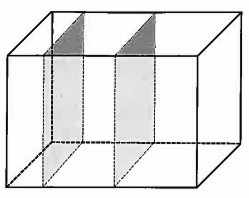
下のような直方体の容器があり、この容器の底面に垂直になるように仕切りを入れます。
仕切りで分けられた３つの部分に同じ量の水を入れたところ、水面の高さがそれぞれ
12ｃｍ、５ｃｍ、４ｃｍになりました。
容器から仕切りをとると水面の高さは何ｃｍになりますか。
ただし、仕切りの厚さは考えないことにします。
 

（４）
弟は一定の速さで家から学校まで歩きます。
兄は弟が出発してから８分後に家を出発して一定の速さで歩きましたが、
途中で一度歩く速くを７/４倍に変えて学校まで歩きました。
すると、弟が出発してから40分後に、兄は弟に追いつき、弟より２分早く学校に到着しました。
このとき、弟が家を出発してからの時間と二人の距離の関係は、下の図のようになります。

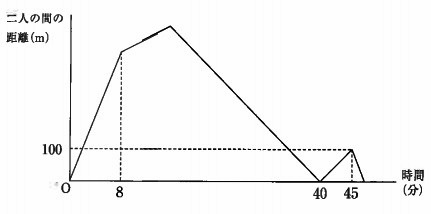
①家から学校までの距離は何ｍですか。

②兄が歩く速さを変えたのは、弟が家を出発してから何分後ですか。

（５）
太郎さんと花子さんが、授業で学んだ内容について話し合いをしています。
太郎：次のような並べ方に従って数を並べたよ。いろいろな決まりがありそうだね。

①下線部①について、４段目の次にすべて奇数が並ぶのは何段目ですか。

②下線部②について、３段目以降の左から３番目の数について考えます。
100段目の左から３番目の数を求めなさい。

（６）
次にように、Ａグループ、Ｂグループにそれぞれ９つの数があります。
Ａグループ【１、２、３、４、５、６、７、８、９】
Ｂグループ【1.1、1.2、1.3、1.4、1.5、1.6、1.7、1.8、1.9】
Ａグループ、Ｂグループの中から数を１つずつ選び、それぞれａ、ｂとします。
このとき、となるａ、ｂの組み合わせは何通りありますか。

掛け算の最初が16、1.6、0.16とケタ違いがあるので、
16×0.875⇒16÷10×0.875×10⇒1.6×8.75
0.16×12.5⇒16×10×12.5÷10⇒1.6×1.25
・・と、1.6×〇に加工する。

16×0.875－1.6×3.75－0.16×12.5
＝1.6×8.75－1.6×3.75－1.6×1.25
＝1.6×（8.75－3.75－1.25）
＝1.6×3.75＝８/５×15/４＝６

⑥
模造紙の大半を占める、地図の縦の長さを求める。
360ｋｍ×45万分の１
＝360,000,00ｃｍ×450.000
＝80ｃｍ
模造紙の残りの縦の長さは、
100－80＝20ｃｍ
これをタイトル：名前＝２：１で分かつので、
タイトルの縦の長さは、20×２/３＝40/３＝13.33…→ウ

⑦
平易な部類に入るので、迅速かつ確実に正解すること！

平行線をひいて錯角でもいけるが、外角定理がわかりやすいかな？
（ア）＝180－（75＋65）＝40°

（２）②
３枚のベン図が重なったときの処理。
重なっている枚数に注目する。
３枚の図形の合計で210ｃｍ²
重なっている状態で全体の面積は148ｃｍ²
210－148＝62ｃｍ²はどこを指すのか？

重なっている枚数が青で、全体の面積をひくと枚数が－１される。
すると、斜線が１枚で、（ア）が２枚。
この合計が62ｃｍ²となる。
よって、斜線部分の合計は62－７×２＝48ｃｍ²

（３）
シンプルだが未経験だと難しい。
同じ量の水を入れたら、高さが12ｃｍ：５ｃｍ：４ｃｍ。
入れた水の量を、これらの最小公倍数である〔60〕とおく。
それぞれの底面積の比は、
〔60〕÷12：〔60〕÷５：〔60〕÷４＝⑤：⑫：⑮
底面積全体の合計は、⑤＋⑫＋⑮＝○32

仕切りをとると、〔180〕の水で底面積が○32だから、
〔180〕÷○32＝45/８ｃｍ

（４）①
まずはグラフの読解。

兄が出発しても兄と弟で距離が開いたということは、
最初の兄の速さは弟よりも遅いことになる。
兄が弟を追い越して学校に到着したとき、弟は学校まで100ｍの地点にいた。
その２分後に到着するので、弟の速さは、100ｍ÷２分＝分速50ｍ
弟は家～学校を47分間で歩いたから、分速50ｍ×47分＝2350ｍ

②
難しめ(;`ω´)
本問のグラフだと気づきにくい糸口があるので、
ダイヤグラムに直したほうがわかりやすい。

兄の速度は、1：７/４＝４：７に変換。
注目すべきは、兄が弟に追いついた40分後。

弟は分速50ｍなので、40分後は学校まで残り50×７＝350ｍ。
歩いた距離は、2350－350＝2000ｍ
残り350ｍを兄は５分で歩ききるので、
兄の速さは、350ｍ÷５分＝分速70ｍ
ここから、⑦＝分速70ｍ、④＝分速40ｍとわかる。
あとは、兄が歩いた速さと時間で鶴亀算。

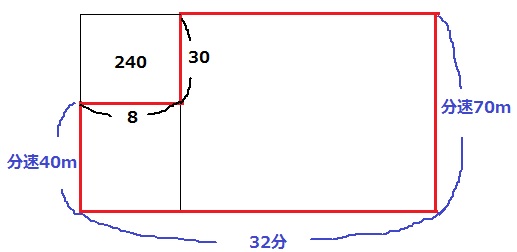
縦が速さ、横が時間、面積が距離。
赤枠の面積が兄が40分間に歩いた距離2000ｍ。
左上の面積が70×32－2000＝240
240÷（70－40）＝８分
したがって、兄が歩く速さを変えたのは、
弟が家を出発してから，８＋８＝16分後

（５）①
二項定理にでてくるパスカルの三角形。
手で書いて調べる。

左右対称なので、半分まで調査すればＯＫ！
次に奇数が並ぶのは、８段目。

②
３段目以降の左から３番目の数を並べてみる。
【１、３、６、10、15、21…】
３段目からスタートなので、100段目はこの数列の98番目にあたる。

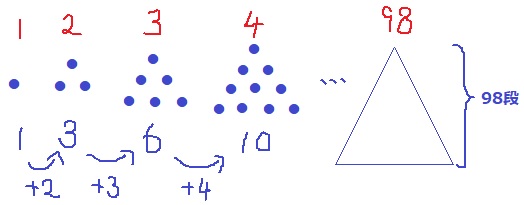
【１、３、６、10、15、21…】の数列は＋２、＋３、＋４…
いわゆる三角数で、上のように図形に置き換えると点の並びが三角形になる。
98番目の数は●が98段になるから、言い換えれば、１～98の総和が答えになる。
（１＋98）×98÷２
＝99×49＝（100－１）×49
＝4900－49＝4851

＠二項定理＠
高校生で習う二項定理を用いると、パスカルの三角形の100段目の数は左から、
₉₉Ｃ₀、₉₉Ｃ₁、₉₉Ｃ₂…となり、₉₉Ｃ₂＝99・98/２＝4851

（６）
ということは分母分子が同じ値なので、ａ＋ｂ＝ａ×ｂ。
つまり、和と積が等しい組合せを選ぶ。

Ａグループ【１、２、３、４、５、６、７、８、９】
Ｂグループ【1.1、1.2、1.3、1.4、1.5、1.6、1.7、1.8、1.9】

Ａグループで１を選ぶと積がｂとなり、積ｂ＜和ａ＋ｂとなるから誤り。
ここからどうすべきか迷う( ;´Д｀)
掛け算をして小数第１位が和と同じになるかをチェックするのだと思われる。
例えば、1.1×２＝1.2は小数第１位が２になる。1.1＋２＝3.1だから×。
1.1×□＝○.1は□＝１だけで、Ａグループで１はダメなので無し（□≠１）。

1.2×□＝○.2　□＝６
1.3×□＝○.3　□＝なし
1.4×□＝○.4　□＝６
1.5×□＝○.5　□＝３、５、７、９
1.6×□＝○.6　□＝６
1.7×□＝○.7　□＝なし
1.8×□＝○.8　□＝６
1.9×□＝○.9　□＝なし
このなかで、実際に積と和が等しくなる組み合わせは、
（ａ、ｂ）＝（６、1.2）（３、1.5）
以上、２通り。
算数の範囲でもっとわかりやすい解法を見つけた方は、
お問い合わせから教えて下さいませ( ;´Д｀)

＠文字式＠
数学を使っても良いのなら、中１（１学期）レベルの数学でもっと楽に解ける。
ａ＋ｂ＝ａ×ｂ
ａ＝ａｂ－ｂ＝ｂ（ａ－１）
ｂ＝ａ/（ａ－１）
ａを整数とする。
→（ａ－１）とａは連続する２つの整数。
ｂは〔ある整数÷１コ手前の整数〕の値となる。

Ａグループ【１、２、３、４、５、６、７、８、９】
Ｂグループ【1.1、1.2、1.3、1.4、1.5、1.6、1.7、1.8、1.9】

ａ＝１　ｂ＝１/０＝×（割る数が０だから）
ａ＝２　ｂ＝２/１＝２（２はＢグループにない×）
ａ＝３　ｂ＝３/２
ａ＝４　ｂ＝４/３
ａ＝５　ｂ＝５/４
ａ＝６　ｂ＝６/５
ａ＝７　ｂ＝７/６
ａ＝８　ｂ＝８/７
ａ＝９　ｂ＝９/８
このなかで、ｂが小数第１位になるのは、
（ａ、ｂ）＝（３、1.5）（６、1.2）
いずれにせよ、時間がかかる。。
後回しにして、他を確実にとった方がいいかも。
難関中（算数科）解説ページに戻る