問題PDF
下の図1のように5×5四方のマス目の中央が塗りつぶされ、
残りのマスに1から24までの番号が順番に書かれたカードがあります。

また、1から24までの番号が1つずつ書かれたボールが入っている袋があります。
この袋の中からボールを1つ取り出し、ボールに書かれた番号と同じ番号のマス目を
塗りつぶすという作業を繰り返します。一度取り出したボールは袋には戻しません。
カードのたて、よこ、ななめのいずれか一列の番号が全て塗りつぶされたとき「終わり」とし、
作業を終了します。例えば図2、図3のように取り出すと「終わり」となります。

(1)
作業をちょうど4回繰り返して「終わり」となるとき、
塗りつぶされた数字の組み合わせは何通りあるか求めなさい。
(2)
作業をちょうど5回繰り返して「終わり」となるとき、
塗りつぶされた数字の組み合わせは何通りあるか求めなさい。
(3)
作業を19回繰り返したとき、1が書かれたマス目は塗りつぶさず、
さらに「終わり」となりませんでした。
このような場合は全部で何通りあるか求めなさい。
またそれらの中の1つを具体的に答えなさい。
ただし、塗りつぶされずに残った数字に丸をつけなさい。

@解説@
(1)
4回で終わる→中央は絶対使う。
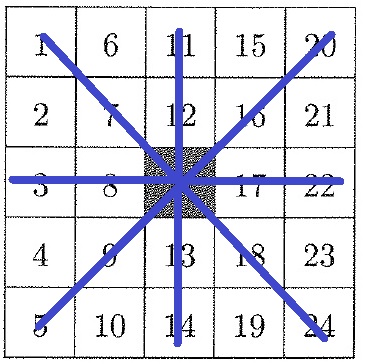
4通り
(2)
5回で終わる→1回スカ+中央を使う4通り(前問)、または中央以外でストレート。
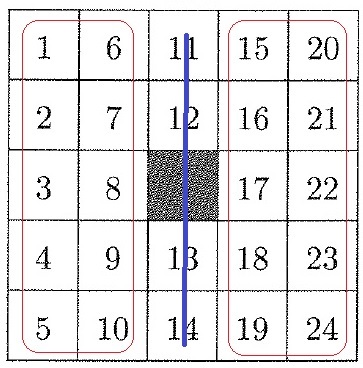
1回のスカは5×4=20通り
中央を使うビンゴは4通りなので、4×20=80通り
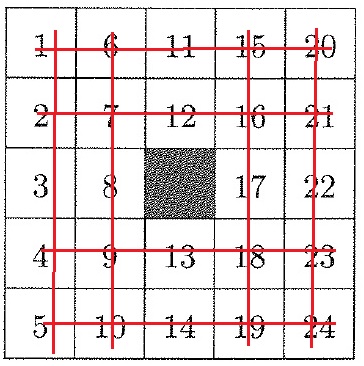
中央を使わないストレートは8通り。
よって、80+8=88通り
(3)
19マス+中央の1マスで20マスが塗りつぶされても終わりにならなかった。
塗りつぶされずに残った5マスを考える。
縦・横・斜め5マスずつのビンゴで、20マス塗りつぶしてもビンゴ不成立ということは、
塗りつぶさない5マスをバラバラに配置させる。
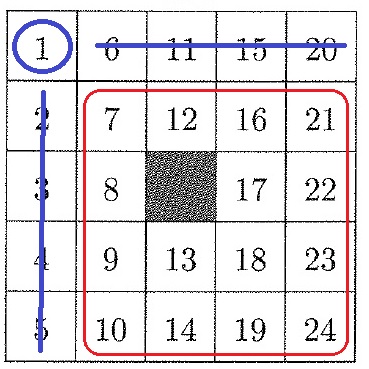
1の縦と横に塗りつぶさないマスを配置すると重複がおきるので、どこかでビンゴしてしまう。×
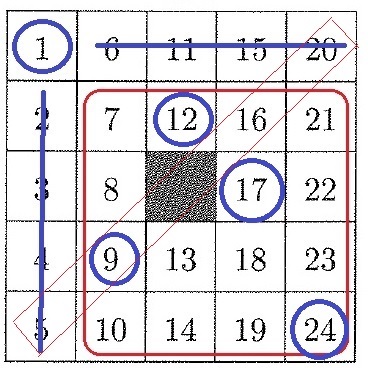
留意すべきは斜め(右上ライン)に塗りつぶさないマスを配置させること。
言い換えれば、9か16には絶対に配置させる。
2行目で7に配置すると9と16に置けないので適さない。
2行目を12にして上のようにすると、縦・横・斜めすべてにおいてビンゴが成立しない。

以上、7通り。
最後の問題で力尽きた生徒が多かったと思われる:;(∩´_`∩);:



コメント