2022年度　東大寺学園中学過去問【算数】大問２解説

問題ＰＤＦ
（１）

図のような通学路に、Ｔ君の家、Ｄ君の家、学校があります。Ｔ君とＤ君は８時にそれぞれの家を出て、それぞれ一定の速さで学校に向かいました。途中のＪ地点を通過したのはＴ君の方が３分早く、学校への到着時刻の差は５分でした。Ｄ君の家からＪ地点までの道のりと、Ｊ地点から学校までの道のりの比が７：３だとすると、Ｔ君がＤ君の家を通過したのは８時何分何秒だったでしょうか。

（２）
整数を異なる３個の整数の積として表すことを考えます。たとえば、24は、
１×２×12、１×３×８、１×４×６、２×３×４
と４通りの表し方があります。
（ⅰ）90を異なる３個の整数の積として表す方法は全部で何通りありますか。
ただし、積の順序だけが異なるものは、それらを全部で１通りとして数えます。

（ⅱ）20以上の整数Ａを、異なる３個の整数の積として表すことはできず、
Ａ＋４も異なる３個の整数の積として表すことはできませんでした。
このような20以上の整数Ａとして考えられるものを小さいものから順に５個答えなさい。

（３）
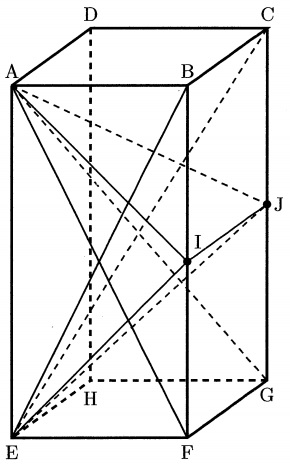
下の図の直方体ＡＢＣＤ―ＥＦＧＨは、ＡＢ＝ＡＤ＝２ｃｍ、ＡＥ＝４ｃｍの直方体で、
Ｉ、ＪはそれぞれＢＦ、ＣＧの真ん中の点です。
このとき、四角すいＡ―ＩＦＧＪと四角すいＥ―ＢＩＪＣの重なっている部分の体積を求めなさい。

＠解説＠
（１）

Ｊ地点ではＴが先に着いて３分差。
学校ではＴが先に着いて５分差。
距離③で２分の差が発生している。
距離に応じて差は比例で拡大する。
距離⑦では、２×⑦/③＝14/３分の差が発生する。

（２）（ⅰ）
１×〇×〇＝90の組み合わせを考えると、
（１、２、45）（１、３、30）（１、５、18）（１、６、15）（１、９、10）
90を素因数分解すると、90＝２×３×３×５
２を残す→（２、３、15）（２、５、９）
３を残す→（３、５、６）
もう無い。
よって、８通り。

（ⅱ）
『異なる３個の整数の積として表せない数』はどんな数か。
思うに、約数が４個以上の数は異なる３個の整数の積で必ず表せる。
たとえば、６の約数は〔１、２、３、６〕で６以外の１×２×３で表せる。
約数の個数が３個以下の数を考える。

まずは素数。
素数の約数は１と自身の２個しかないので表せない。
もう１つは素数の平方数。
たとえば、３×３＝９の約数は〔１、３、９〕の３個で、９＝１×９＝３×３しかない。

20以上の素数or素数の平方数を探し、その＋４もそうでないか調べあげる。
23は素数。しかし27は×。
25は素数の平方数。29も素数。〇
29は素数。しかし33は×！
31は素数。35×！
37は素数。41も素数！〇
41は素数だが45が×です。
43は素数で、47も素数！〇
47は素数だけど、51が違います。×
49が素数の平方数であることを忘れてはならない。53は素数！〇
53は素数で57は×。
59は素数で63が違う。×
61⇒65×！
67⇒71〇！
したがって、25、37、43、49、67
５個も出させるなんて(∩´﹏`∩)

（３）
難関校で出題される共通部分の問題。

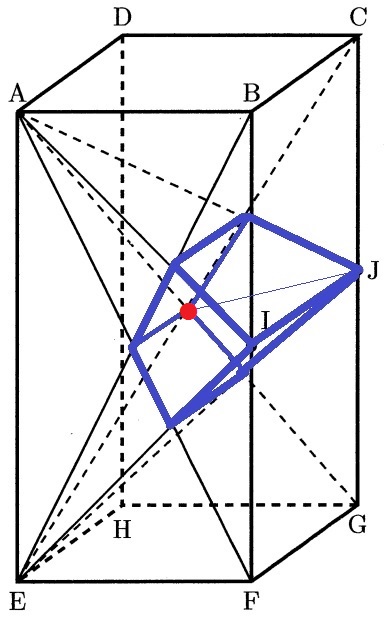
求積すべき立体はこうなる。
手前の四角形は長方形ＡＥＦＢ上にあるが、背面の扱いに注意！
Ａは前方の上から奥の下側へ、Ｅは前方の下から奥の上側へスポットライトを当てる。
奥へ向かうＡＧとＥＣの交点●から上下に分かれるので、
背面は１つの面ではなく、屋根みたいに２面に分かれる。
立体は断頭四角柱ではなく、合同な２つの断頭三角柱を上下に合わせた感じになる。

うえのような記号をふる。
底面積は四角形ＭＫＯＩ。
△ＡＥＭと△ＢＩＭが相似で、ＡＭ：ＭＩ＝②：①
△ＡＥＩと△ＭＯＩの相似で、ＭＯ＝４×①/③＝４/３ｃｍ
ＫＩ＝２÷２＝１ｃｍ
ＭＯとＫＩは菱形の対角線のように直交する。
四角形ＭＫＯＩの面積は、４/３×１÷２＝２/３ｃｍ²

高さは断頭三角柱の平均の高さで攻略する。
ＩＪ＝２ｃｍ
△ＡＫＬと△ＡＦＧが相似→ＫＬ＝２÷２＝１ｃｍ
△ＡＭＮと△ＡＩＪが相似→ＭＮ＝２×②/③＝４/３ｃｍ
高さの平均は、（２＋１＋４/３）÷３＝13/９ｃｍ

求積すべき立体の底面積は２/３ｃｍ²、高さの平均は13/９ｃｍで、
上下の断頭三角柱を一括して求めると、その体積は２/３×13/９＝26/27ｃｍ³
難関中（算数科）解説ページに戻る