問題ＰＤＦ
次の文章を読み、〔 ア 〕～〔 オ 〕にあてはまる数をそれぞれ答えなさい。
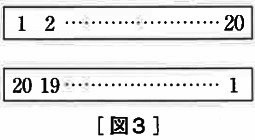
Ａ君は、〔図３〕のような２枚の長方形の紙を利用して、１から20までの和を求めたところ、１＋２＋３＋･･･＋20＝〔 ア 〕となりました。
さらにＡ君は、１×１＋２×２＋３×３＋･･･20×20を求める方法を先生から教わりました。先生は正三角形の紙に〔図４〕のように、上から１段目に１を１個、２段目に２を２個、３段目に３を３個、･･･、20段目に20個書きました。そうすると、正三角形の紙に書かれた数の和を求めればよいことになります。
次に先生は、〔図４〕の紙を３枚用意し、〔図５〕のように並べました。
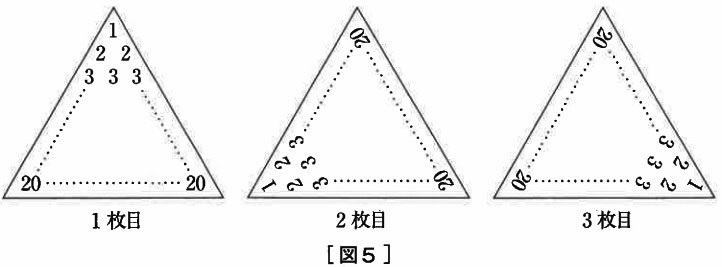
１枚目、２枚目、３枚目の上から１段目に書かれた３つの整数の和は〔 イ 〕です。
また、１枚目、２枚目、３枚目の上から２段目の左に書かれた３つの整数の和は〔 ウ 〕です。
このことに注目すると、
１×１＋２×２＋３×３＋･･･＋20×20＝〔 イ 〕×〔 エ 〕÷３＝〔 オ 〕となります。
＠解説＠
高校数学で習う２乗和の公式。
アは１～20までの和。
（１＋20）×20÷２＝210
ア…210
誘導に従う。
１段目（一番上）の合計は、１＋20＋20＝41になる。
イ…41
上から２段目の左に書かれた数字の和（一番上の左下）は、
２＋19＋20＝41
ウ…41
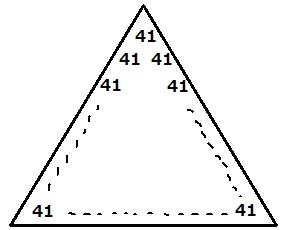
３枚の正三角形を重ね合わせると、すべて41。
41の個数は、１段目が１個。２段目が２個。３段目が３個…20段目が20個。
つまり、アで求めた1～20の和である210個の41がある。
エ…210
合計は正三角形３つを重複してカウントしているので、最後に÷３をする。
41×210÷３＝2870
オ…2870
１段目に１が１個、２段目に２が２個、３段目に３が３個‥20段目に20が20個つづく正三角形の和が１×１+２×２+３×３+…+20×20の値になるが、１枚の正三角形では総和を求められないので、120°回転させた２枚の正三角形を別に作り、３枚を合わせると全ての数が同じになることを利用する。
＠総和を求める公式＠
１乗和の公式（１＋２＋･･･ｎ）＝ｎ（ｎ＋１）/２
２乗和の公式（１×１＋２×２･･･ｎ×ｎ）＝ｎ（ｎ＋１）（２ｎ＋１）/６
↑１乗和の公式を使い、本問の考えで計算するとこのようになる。
３乗和の公式（1×1×1＋2×2×2＋ｎ×ｎ×ｎ）＝{ｎ（ｎ＋１）/２}2
３乗和は１乗和の値を２回かけるだけで出せてしまう。
（ex.１～20までの３乗和の場合。１～20の１乗和が210だから、３乗和は210×210＝44100）
３乗和でも幾何の発想で公式を導くことができます。詳しくはコチラ→ロボット・ＩＴ雑食日記
３乗和が１乗和の２乗。
２乗ということは正方形の面積で考える。
１×１×１が青の正方形。
２×２×２は２×２の正方形が２つあり、１つを半分にわけてくっつけると、
青＋緑の正方形の面積となる。
３×３×３は３×３の正方形を３つくっつける（オレンジ）。
４×４×４は４×４の正方形が４つあり、１つを半分にわけてくっつける（赤）。
全体の正方形をみると、１辺が１の正方形、１＋２の正方形、１＋２＋３の正方形、１＋２＋３＋４の正方形…と広がっていくので、３乗和は１乗和の２乗となる。
面白い発想ですね(*’ω’*)
江戸川取出で３乗和の問題が出題されています。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント