問題PDF
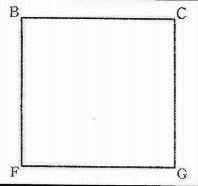
下の図1のような1辺の長さが10cmの立方体ABCD-EFGHについて、次の問いに答えなさい。

(1)
立方体の辺上または内部の点P、Q、Rをとって、7つの点P、Q、R、E、F、G、Hを頂点として、
三角形PQR、正方形EFGHといくつかの多面体を面にもつ立体Xを考えます。
この立体Xを(あ)の方向から見ると図2、(い)の方向から見ると図3、(う)の方向から図4のように見えます。
図3、図4でPとQは重なって見えていて、辺DHの真ん中の点とも重なって見えます。
また、Rは辺DGに重なって見えます。

(ア)
立体Xを図1の(え)の方向から見たときの図を解答欄にかきなさい。
(イ)
立体Xの面の数はいくつですか。
(ウ)
立体Xの体積は何cm3ですか。
(2)
立体の内部に2点S、Tをとり、図1の(あ)と(い)の方向からこの2点をみると、
図5のように見えます。2つの図でS、Tは正方形の対角線を3等分する点とします。
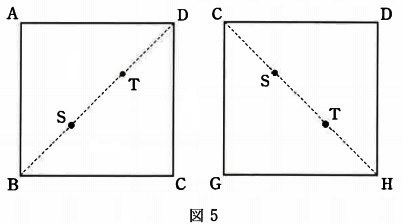
このとき、4点F、G、T、Sを頂点とする立体Yの体積は何cm3ですか。
@解説@
(1)

P、Q、Rの位置を確認しよう。
PはAE上の中点、QはDH上の中点、Rは真上からみて中心にある。
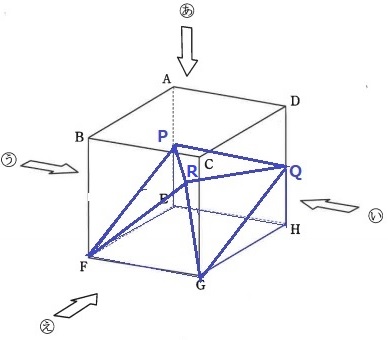
これを思い浮かべられないと点差が開いてしまう。
(ア)
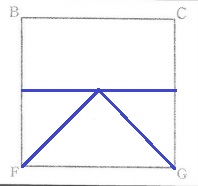
(イ)
面の数は8個。
(ウ)
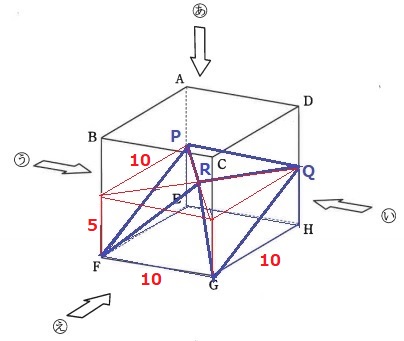
立方体の下半分から、三角錐2つと四角錘1つをひく。
10×10×10÷2-(5×10÷2×5÷3×2+5×10×5÷3)
=1000/3cm3
(2)
ここも出だしの空間認識が肝要。
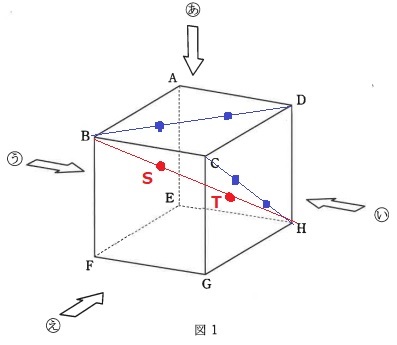
S、Tは立方体の対角線BH上にくる。
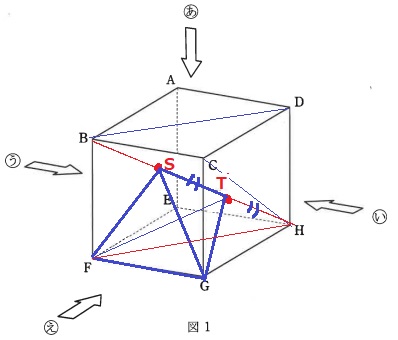
三角錐S-FGTを求めたい。
SとTがBH上にあるということは、S、T、Fは面BFH上にある。
三角錐S-FGHと三角錘T-FGHは底面を△FGHで共通し、
ST=THより高さが2:1なので、S-FGH:T-FGHの体積比は2:1。
ということは、S-FGHからT-FGHをひいたS-FGTはT-FGHと体積が等しい。
10×10÷2×(10×1/3)÷3=500/9cm3



コメント