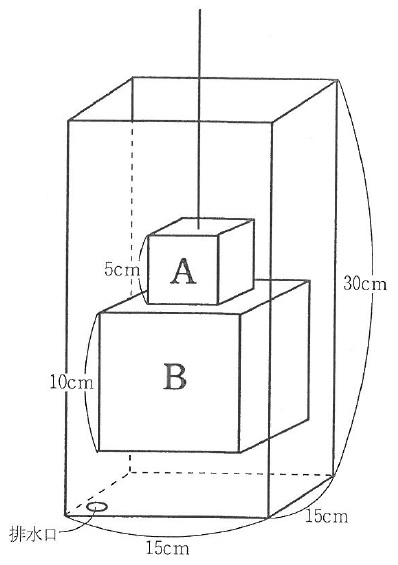
下の図のように、立方体Ａ、Ｂをはなれないようにくっつけて重りを作り、直方体の透明な水そうの中にひもでつるします。
重りの下の面は水そうの底面から５ｃｍのところにあり、常に水そうの底面と平行です。
水そうの中は、最初水で満たされていて、底面の排水口から毎秒50ｃｍ3の割合で排水します。また、排水を始めると同時に、重りをつるしたひもを毎秒１/２ｃｍの速さで、上にひきあげます。ただし、水の浮力やひもの体積、水そうの厚みは考えないものとします。ひもはのびたり、たるんだりしません。
（１）
水面の高さがＡの上の面より１ｃｍ上になるのは、排水を始めてから何秒後ですか。
（２）
水面の高さがＡの上の面より１ｃｍ上になったとき、今度はひもを毎秒１/２ｃｍの速さで下ろすことにします。排水は変わらずに続け、重りは排水口をふさぎません。重りが水そうの底面に着地した後は、ひもを動かさず、排水だけ続けます。
①
重りが水そうの底面に着地したとき、水面は水そうの底面から何ｃｍのところにありますか。
②
排水を始めてから75秒後、残っている水の体積は何ｃｍ3ですか。
このとき水面は水そうの底面から何ｃｍのところにありますか。
＠解説＠
（１）
横から眺めると以下の感じ。
水槽の底面は15×15ｃｍ2なので、
１秒間に下がる水面の速さは、50ｃｍ3÷（15×15ｃｍ2）＝２/９ｃｍ
Ａの上面と水面は毎秒２/９＋１/２＝13/18ｃｍずつ縮まっていく。
９ｃｍ縮まるのは、９÷13/18＝162/13秒後（12・６/13秒後）
（２）①
初期状態（重りを上げ始めて）から（１）までに162/13秒後。
そこから下がって初期状態までは162/13秒後。
さらに10ｃｍを毎秒１/２ｃｍで下がるので、重りが底面に着地するのは、
162/13×２＋10÷１/２＝454/13秒後
水面は毎秒２/９ｃｍずつ下がり、これは重りを下げるスピードより遅い。
（重りは常に水面下にある）
水面が下がる高さは、毎秒２/９ｃｍ×454/13秒＝908/117ｃｍ
よって、重りが着地したときの水面の高さは、
30－908/117＝2602/17ｃｍ（22・28/117ｃｍ）
ｲﾗｲﾗｲﾗｲﾗ~(#ﾟДﾟ)
②
水槽の体積…15×15×30＝6750ｃｍ3
２つの重りの体積…10×10×10＋５×５×５＝1125ｃｍ3
はじめにあった水の体積…6750－1125＝5625ｃｍ3
75秒間に排水された水…50×75＝3750ｃｍ3
残る水…5625－3750＝1875ｃｍ3
重りＢの周りの体積…
（15×15－10×10）×10＝1150ｃｍ3
残りの水…1875－1150＝725ｃｍ3
重りＡがあるところの底面積…15×15－５×５＝200ｃｍ2
したがって、10ｃｍ＋725ｃｍ3/200ｃｍ2＝10＋25/８＝105/８ｃｍ（13・１/８ｃｍ）
桜蔭は他の設問でも忙殺する計算量が求められるので、
我慢強さと集中力、処理能力がないと心が折られます。。。
難関中（算数科）解説ページに戻る
コメント