問題PDF
1からAまでの整数を左から小さい順に並べます。
これらをつなげて、ひとつの長い数字の列を作りました。
123456789101112・・・
次のとき、2021という数字の並びは何回あらわれますか。
(1)A=99
(2)A=9999
(3)A=99999
@解説@
(1)
1~99のうち、2021の並びは〔20〕〔21〕しかない。
2桁ずつ〔□2〕〔02〕〔1□〕と区切ってしまうと、
あいだに〔02〕がでてしまうので、これ以外はない。
1回
(2)
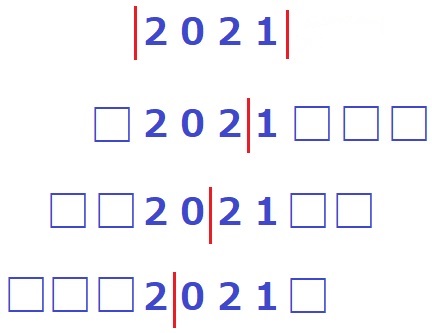
↑こういうふうに□を書いて調べてみよう。
あとは虫食い算のように穴を埋めていく。
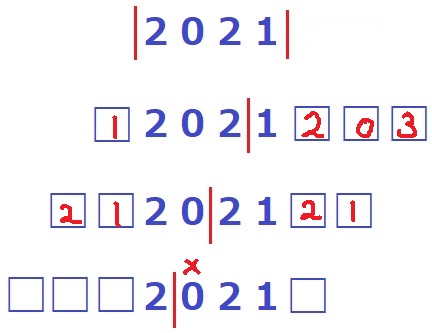
最高位に0がくるのは×。
3回しかない。
前問の答えを足し忘れないように!
4回
@余談@
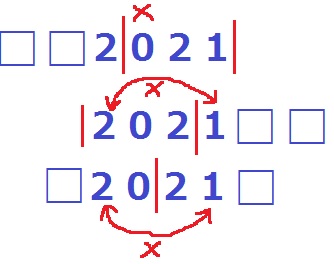
なぜ2桁から4桁に飛んだのかというと、3桁区切りだと回数が増えないからです。
(3)

最高位に0がつかえないので、下4ケタが2021は9回
下3ケタが202は万の位が1。千の位は0~9で10回
同様に、下2ケタが20も百の位が0~9で10回
最後は20210番台で10回
計39回
前問と足し合わせて43回



コメント