問題PDF
下の図のように、幅6mの歩道と車道があり、歩道内の図の位置に柱が立っています。
また、車道の真ん中を幅2mの車が上方から下方に向かって走っています。
歩道、車道とも十分に長いものとします。
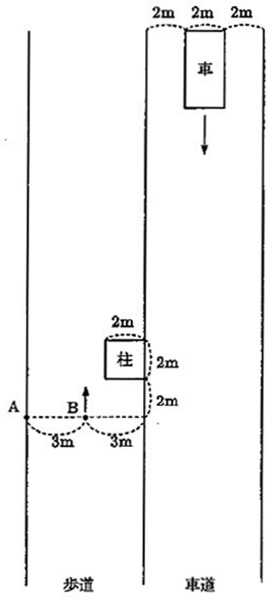
(1)
太郎君が図の地点Aに立って車を見ているとき、
車の長さが〔 〕m以下であれば、車が柱のかげに完全に隠れる瞬間があります。
以下では車の長さを4mとし、車の速さを毎秒4.5mとします。
(2)
太郎君が図の地点Bに立って車を見ているとき、
車が柱のかげに完全に隠れてから〔 〕秒後に車の一部が見え始めます。
(3)
太郎君が地点Bに立っていて、車が柱のかげに完全に隠れると同時に、
矢印の方向に毎秒1mの速さで歩道の真ん中を歩き始めました。
車の一部が見え始めるのは、太郎君が歩き始めてから〔 〕秒後です。
@解説@
(1)
Aから見た、死角の範囲を作図する。
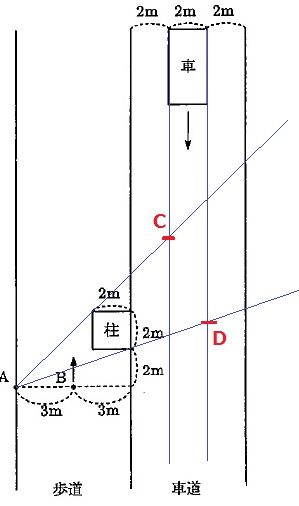
気をつけるべき点は、死角への出入りが車の左右で違うこと!
車の進行方向の右側がC点で死角に入り、進行方向の左側がD点で死角から出てくる。
求めるべき長さはCD間の縦方向の長さにあたる。

ごちゃごちゃして申し訳ない(; ̄Д ̄)
△AEF∽△AGC(∽→相似)より、CG=8m
△AHI∽△AJDより、DJ=10/3m
したがって、8-10/3=14/3m
(2)
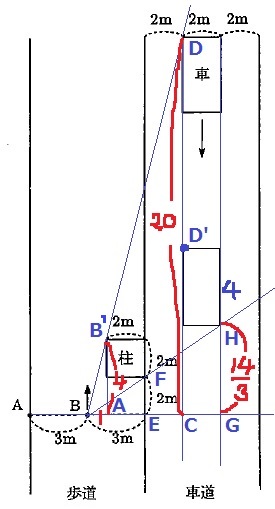
(↑Bが重複してしまったのでB’にしました)
車が点Dで死角に入り、点Hで死角からあらわれる。
△BAB’∽△BCD(∽=相似)より、CD=20m
△BEF∽△BGHより、GH=14/3m
留意点は、車が動いた距離はDD’間で、DH間の縦の長さから車体分を引くこと!
20-14/3-4=34/3m
車の速さは毎秒4.5mだから、34/3÷4.5=68/27秒後
(3)
さらに大変:;(∩´_`∩);:
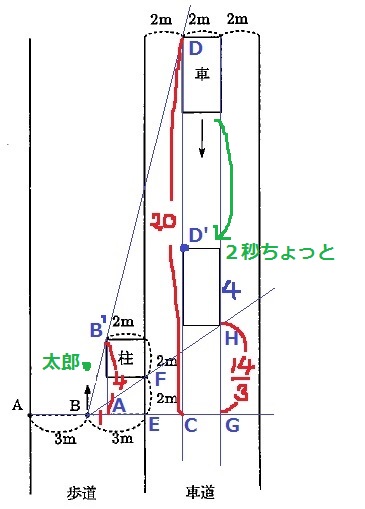
車が柱に完全に隠れてから太郎が歩き出す。
車の方が速く、68/27秒後(2秒ちょっと)でDがD’へ移動するが、
太郎が2秒ちょっと動くと柱をはさんで太郎と車が反対側にあり、車は死角の中にある。
この状態からさらに時間を進めていくと、太郎視点で車の一部が見え始めるのは、
太郎が柱を過ぎ、後ろを眺めると車の進行方向の右側があらわれたとき。
(死角の範囲は太郎のスピードに合わせて動く。
太郎と車の速さの比は、太郎:車=1:4.5=2:9
車の方が4倍以上速いので車が死角から出て行く形になり、右側がいち早くみえる)
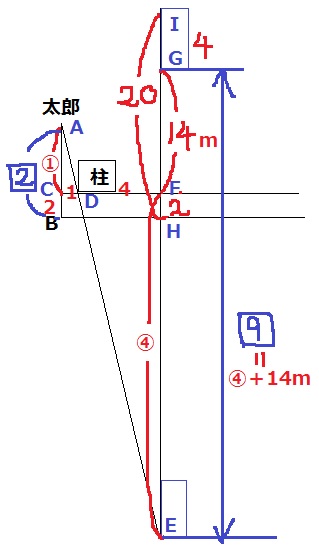
長さを認定していくと上の図になるが、かなり手厳しい。
△ACD∽△EFDより、AC:EF=CD:FD=1:4
太郎が動いた距離□2は、①+2mとなる。
前問より、IH=20m
GF=20-4-2=14m
車が動いた距離□9は、④+14mになる。
□2=①+2mなので、□9=(①+2)×9/2=○9/2+9m
○9/2+9=④+14
○1/2=5
①=10m
太郎が歩いた距離は、10+2=12m
毎秒1mで歩くので、12秒後となる。



コメント