問題ＰＤＦ
☆を１けたの整数として、次のような操作を行います。
【操作；ある整数の一の位を消してできる新たな整数から、消した一の位の☆倍を引く】
整数にこの操作をくり返して０になるとき、この整数を「☆の仲間」と呼ぶことにします。
たとえば、☆を９とします。
1001にこの操作をくり返すと、1001→91→０となるので、1001は「９の仲間」です。
一方、1002→82、2020→202→２となるので、1002も2020も「９の仲間」ではありません。
（１）
4567654→〔 ア 〕→〔 イ 〕→〔 ウ 〕→〔 エ 〕→０となるので、
4567654は「９の仲間」です。ア～エに入る整数はそれぞれ何ですか。
（２）
10けたの整数45676〔オ〕4404は「９の仲間」です。
オに入る１けたの整数は何ですか。
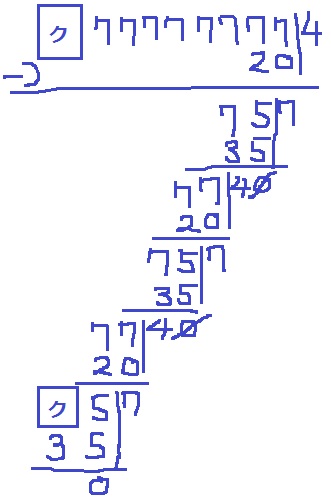
☆を５として、34323にこの操作をくり返すと、34323→3417→306→０となるので、
34323は「５の仲間」です。
（３）
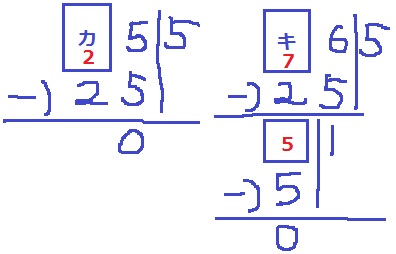
３けたの整数〔カ〕55、〔キ〕65はともに「５の仲間」です。
カ、キに入る１けたの整数はそれぞれ何ですか。
（４）
10けたの整数〔ク〕777777774は「５の仲間」です。
クに入る１けたの整数は何ですか。
（５）
10けたの整数〔ケ〕〔ケ〕333333〔コ〕〔コ〕は「５の仲間」です。
ケ、コに入る１けたの整数を１組求めなさい。
＠解説＠
（１）
一の位を除外して、一の位×９を引きつづける。
０だったらその場で消しています。
ア…456729、イ…45591、ウ…4550、エ…455
（２）
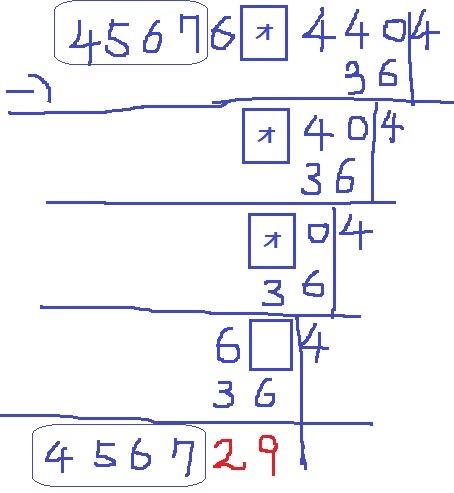
先ほど〔456729〕が９の仲間だったので、途中の末尾が29になればいい。
不明な場所を空欄にして、29の手前まで処理をおこなう。
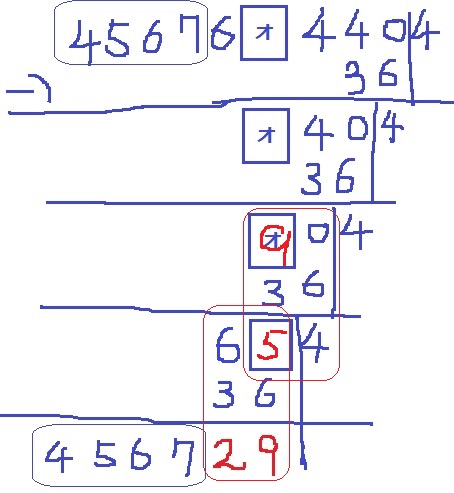
あとは虫食い算の要領で、29＋36＝65→□＝５
54＋36＝90→オ＝９
（３）
同様に虫食い。
カ…２、キ…７
（４）
途中で繰り返しがある。ク＝３
（５）
難しい。
どこかに取っ掛かりはないか…今まで出てきた５の仲間を観察する。
34323→3417→306→０
255→０
765→51→０
3777777774→…→774→357→０
最後が51の倍数!
試しに他の数字も割ってみると、５の仲間はすべて51で割り切れる。
ということは、〔ケ〕〔ケ〕333333〔コ〕〔コ〕も51の倍数になるはず。
しかし、ここで手が詰まる(;´･ω･)
以下、力業です。。
◆ケ＝１のとき
ひとまず、コ＝０とおきます。
1.133.333.300÷51＝22.222.221…29
余り51にするには、51－29＝22を足せばいい。
＠コの余りパターン＠
11…余り11、22…余り22、33…余り33、44…余り44、55…余り４、
66…余り15、77…余り26、88…余り37、99…余り48
1.133.333.322÷51＝22.222.222で割り切れる。
ケ＝１、コ＝０（１個目）
◆ケ＝２のとき
面倒くさいが…1.100.000.000÷51＝21.568.627…23
ケを＋１する（＋1.100.000.000）と、余りが＋23になる。
余り29＋余り23－51＝余り１
51の倍数にするには＋余り50だがない。×
◆ケ＝３のとき
余り１＋余り23＝余り24
51－24＝27はない×
２桁の整数は99まであるが、さらに51を足しても78はない×
◆ケ＝４のとき
余り24＋余り23＝余り47
51－47＝４
コ＝５のとき、余り４となる。〇
ケ＝４、コ＝５（２個目）
◆ケ＝５のとき
余り47＋余り23－51＝余り19
51－19＝32ない×
32＋51＝83×
◆ケ＝６のとき
余り19＋余り23＝余り42
51－42＝９×
９＋51＝60×
◆ケ＝７のとき
余り42＋余り23－51＝余り14
51－14＝37！
コ＝８のとき余り37だから成立。
ケ＝７、コ＝８（３個目）
◆ケ＝８のとき
余り14＋余り23＝余り37
51－37＝14×
14＋51＝65×
◆ケ＝９のとき
余り37＋余り23－51＝余り９
51－９＝42×
42＋51＝93×
したがって、（ケ、コ）＝（１、２）（４、５）（７、８）
＠余談＠
本問は１組見つければ正解になりますが…もっと効率良いやり方がありそう(;´Д｀)
粘ったのですがサボの限界です。無念
はじめはコに注目して、51の倍数の下二桁でありえない組み合わせを探してみました。
〔51、102、153、204、255、306、357、408、459〕
偶数は同じ数をかければゾロ目に（たとえば22だったら51×22）
11であれば51×61、33は51×83、55は51×…05、77は51×27、99は51×49
０以外はすべて作れる。
あとは51＝３×17なので、ケ＋コが３の倍数になるくらい。
前問の3777777774から規則を見出すものかな～と思いきや何も発見できず…。
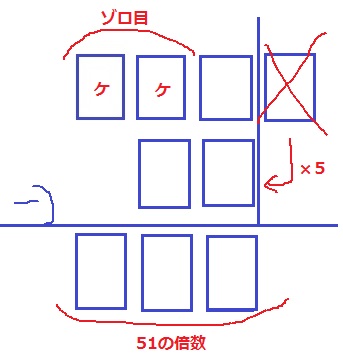
コを確定させないとケ側の処理ができないと思うんだけどなぁ。。
良い解法を編み出した方は、コメント欄かお問い合わせよりお知らせ願います。
難関中（算数科）解説ページに戻る
コメント